Note

This page is a reference documentation. It only explains the class signature, and not how to use it. Please refer to the user guide for the big picture.

nilearn.glm.SimpleRegressionResults

class nilearn.glm.SimpleRegressionResults(results)

Contain only information of the model fit necessary for contrast computation.

Its intended to save memory when details of the model are unnecessary.

__init__(results)

See LikelihoodModelResults constructor.

The only difference is that the whitened Y and residual values are stored for a regression model.

logL()

Return the maximized log-likelihood.

residuals(Y, X)

Residuals from the fit.

Fcontrast(matrix, dispersion=None, invcov=None)

Compute an F contrast for a contrast matrix matrix.

Here, matrix M is assumed to be non-singular. More precisely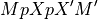

is assumed invertible. Here, 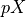is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full.

See the contrasts module to see how to specify contrasts. In particular, the matrices from these contrasts will always be non-singular in the sense above.

Parameters:

matrix1D array-like

Contrast matrix.

dispersionNone or float, optional

If None, use self.dispersion.

invcovNone or array, optional

Known inverse of variance covariance matrix. If None, calculate this matrix.

Returns:

f_resFContrastResults instance

with attributes F, df_den, df_num

Notes

For F contrasts, we now specify an effect and covariance.

Tcontrast(matrix, store=('t', 'effect', 'sd'), dispersion=None)

Compute a Tcontrast for a row vector matrix.

To get the t-statistic for a single column, use the ‘t’ method.

Parameters:

matrix1D array-like

Contrast matrix.

storesequence, default=(‘t’, ‘effect’, ‘sd’)

Components of t to store in results output object.

dispersionNone or float, optional

Returns:

resTContrastResults object

conf_int(alpha=0.05, cols=None, dispersion=None)

Return the confidence interval of the specified theta estimates.

Parameters:

alphafloat, default=0.05

The alpha level for the confidence interval. ie., alpha = .05 returns a 95% confidence interval.

colstuple, optional

cols specifies which confidence intervals to return.

dispersionNone or scalar, optional

Scale factor for the variance / covariance (see class docstring and vcov method docstring).

Returns:

cisndarray

cis is shape (len(cols), 2) where each row contains [lower, upper] for the given entry in cols

Notes

Confidence intervals are two-tailed.

tailsstring, optional

Possible values: ‘two’ | ‘upper’ | ‘lower’

Examples

>>> from numpy.random import standard_normal as stan
>>> from nilearn.glm import OLSModel
>>> x = np.hstack((stan((30, 1)), stan((30, 1)), stan((30, 1))))
>>> beta = np.array([3.25, 1.5, 7.0])
>>> y = np.dot(x, beta) + stan((30))
>>> model = OLSModel(x).fit(y)
>>> confidence_intervals = model.conf_int(cols=(1, 2))

normalized_residuals(Y, X)

Residuals, normalized to have unit length.

See Montgomery et al.[1] and Davidson and MacKinnon[2].

Notes

Is this supposed to return “standardized residuals,” residuals standardized to have mean zero and approximately unit variance?

d_i = e_i / sqrt(MS_E)

Where MS_E = SSE / (n - k)

References

[1]

Douglas C. Montgomery, Elizabeth A. Peck, and Geoffrey G. Vining. Introduction to Linear Regression Analysis (4th ed.). Wiley & Sons, 2006. ISBN 0471754951.

[2]

Russell Davidson and James G. MacKinnon. Econometric theory and methods. Oxford Univ. Press, New York, NY [u.a.], 2004. ISBN 978-0-19-512372-2.

t(column=None)

Return the (Wald) t-statistic for a given parameter estimate.

Use Tcontrast for more complicated (Wald) t-statistics.

vcov(matrix=None, column=None, dispersion=None, other=None)

Return Variance/covariance matrix of linear contrast.

Parameters:

matrix(dim, self.theta.shape[0]) array, optional

Numerical contrast specification, where dim refers to the ‘dimension’ of the contrast i.e. 1 for t contrasts, 1 or more for F contrasts.

columnint, optional

Alternative way of specifying contrasts (column index).

dispersionfloat or (n_voxels,) array, optional

Value(s) for the dispersion parameters.

other(dim, self.theta.shape[0]) array, optional

Alternative contrast specification (?).

Returns:

cov(dim, dim) or (n_voxels, dim, dim) array

The estimated covariance matrix/matrices.

Returns the variance/covariance matrix of a linear contrast of the

estimates of theta, multiplied by dispersion which will often be an

estimate of dispersion, like, sigma^2.

The covariance of interest is either specified as a (set of) column(s)

or a matrix.

predicted(X)

Return linear predictor values from a design matrix.