9.2. Manipulating images: resampling, smoothing, masking, ROIs…

This chapter discusses how nilearn can be used to do simple operations on brain images.

9.2.1. Functions for data preparation and image transformation

Nilearn comes with many simple functions for simple data preparation and transformation. Note that if you want to perform these operations while loading the data into a data matrix, most are also integrated in the masker objects.

9.2.2. Resampling images

9.2.2.1. Resampling one image to match another one

nilearn.image.resample_to_img resamples an image to a reference image.

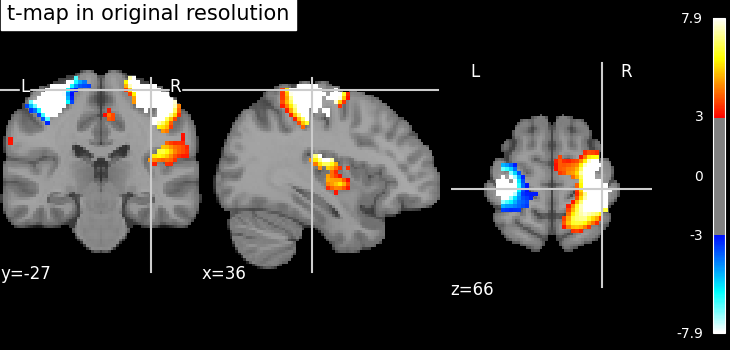
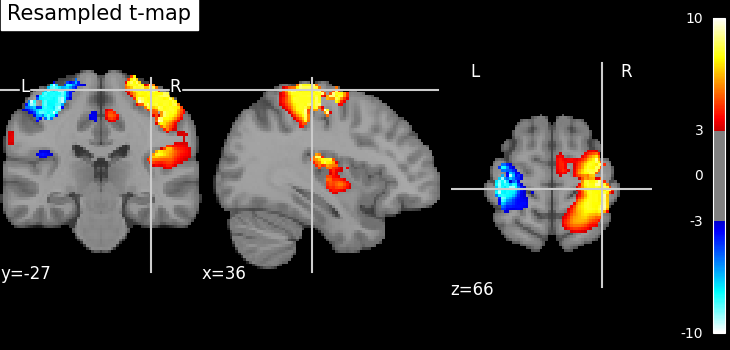
../_images/sphx_glr_plot_resample_to_template_001.png ../_images/sphx_glr_plot_resample_to_template_002.png

This can be useful to display two images as overlays in some viewers (e.g., FSLView) that require all images to be on the same grid.

9.2.2.2. Resampling to a specific target affine, shape, or resolution

nilearn.image.resample_img specifies the resampling in terms of the target_affine to match the spatial configuration defined by the new affine.

Additionally, a target_shape can be used to resize images (i.e., cropping or padding with zeros) to match an expected data image dimensions (shape composed of x, y, and z).

Resampling can be useful to downsample images to increase processing speed and lower memory consumption.

On an advanced note, automatic computation of offset and bounding box can be performed by specifying a 3x3 matrix instead of the 4x4 affine. In this case, nilearn computes automatically the translation part of the transformation matrix (i.e., affine).

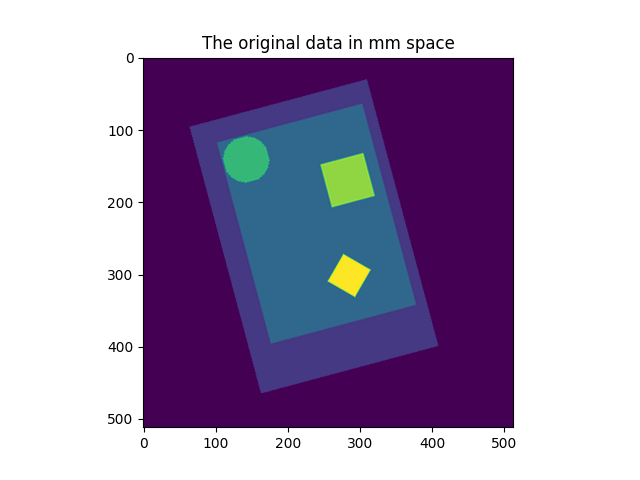
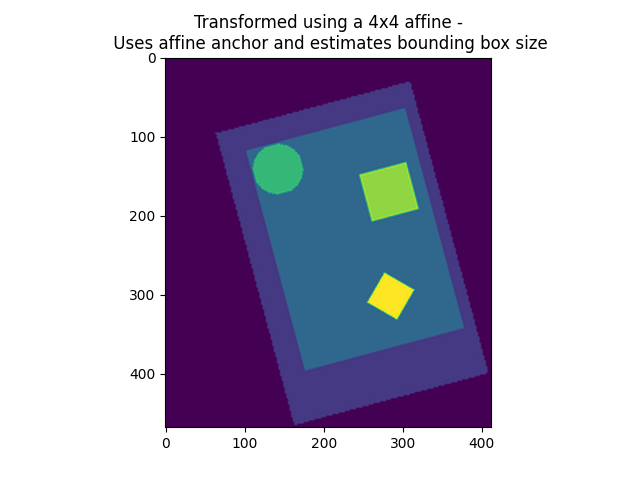
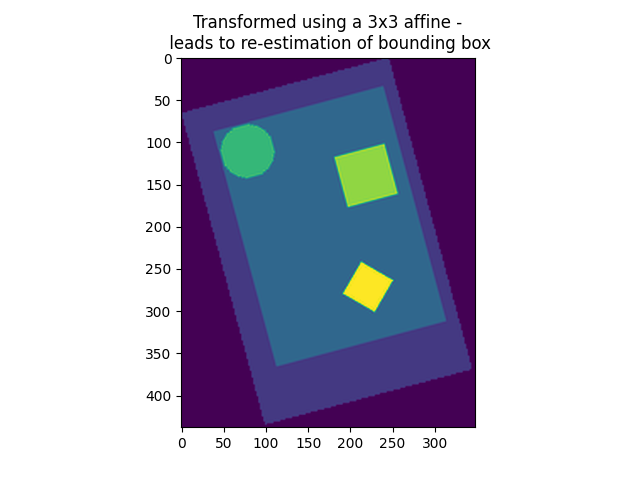
../_images/sphx_glr_plot_affine_transformation_002.png ../_images/sphx_glr_plot_affine_transformation_004.png ../_images/sphx_glr_plot_affine_transformation_003.png

See also

An example illustrating affine transforms on data and bounding boxes

9.2.3. Accessing individual volumes in 4D images

See also

  • nilearn.image.concat_imgs: merge multiple 3D (or 4D) images into one 4D image by concatenation along the 4th (time) axis

  • nilearn.image.load_img: load an image into memory. The benefit of this function is that it will convert various representations, such as filename, list of filenames, wildcards, list of in-memory objects, to an in-memory NiftiImage.

  • nilearn.image.new_img_like: given data in a numpy array, creates a new image using an existing reference image for the metadata.


9.2.4. Computing and applying spatial masks

Relevant functions:

9.2.4.1. Extracting a brain mask

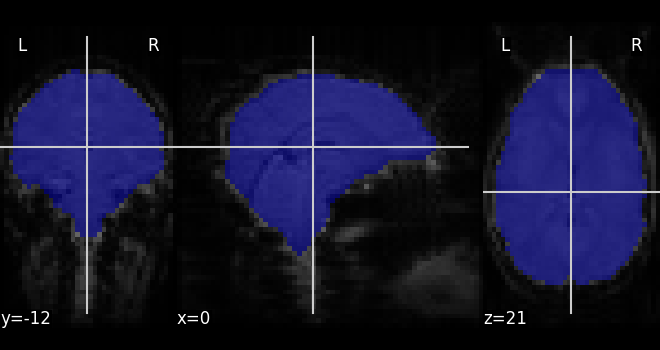
If we do not have a spatial mask of the target regions, a brain mask can be computed from the data:

from nilearn.masking import compute_epi_mask

mask_img = compute_epi_mask(func_filename)

# Visualize it as an ROI
from nilearn.plotting import plot_roi

plot_roi(mask_img, mean_haxby)

# %%
../_images/sphx_glr_plot_visualization_002.png

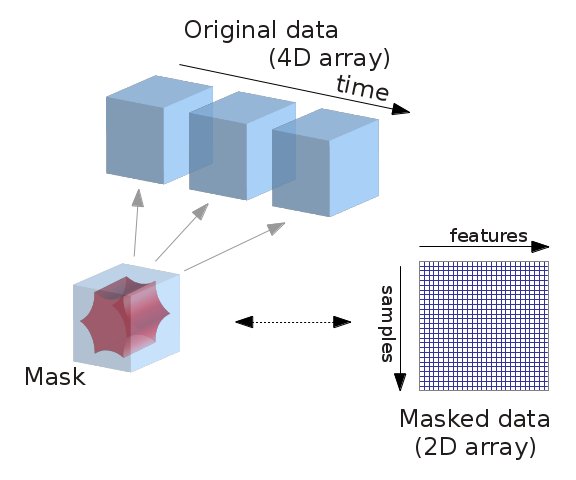
9.2.4.2. Masking data: from 4D Nifti images to 2D data arrays

fMRI data is usually represented as a 4D block of data: 3 spatial dimensions and one time dimension. In practice, we are usually interested in working on the voxel time-series in the brain. It is thus convenient to apply a brain mask in order to convert the 4D brain images representation into a restructured 2D data representation, voxel x time, as depicted below:

../_images/masking.jpg

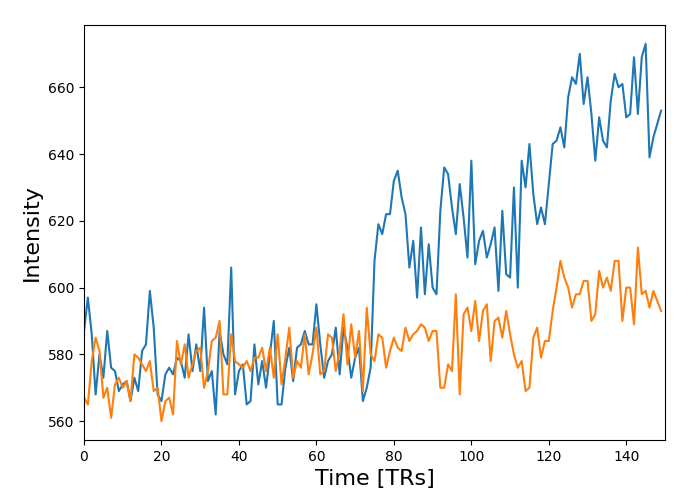
Note that in an analysis pipeline, this operation is best done using the masker objects. For completeness, we give the code to do it manually below:

# ----------------------------------------------------------
from nilearn.masking import apply_mask

masked_data = apply_mask(func_filename, mask_img)

# masked_data shape is (timepoints, voxels). We can plot the first 150
# timepoints from two voxels

# And now plot a few of these
import matplotlib.pyplot as plt

plt.figure(figsize=(7, 5))
plt.plot(masked_data[:150, :2])
plt.xlabel("Time [TRs]", fontsize=16)
plt.ylabel("Intensity", fontsize=16)
plt.xlim(0, 150)
plt.subplots_adjust(bottom=0.12, top=0.95, right=0.95, left=0.12)

show()

# sphinx_gallery_dummy_images=3
../_images/sphx_glr_plot_visualization_003.png

9.2.5. Image operations: creating a ROI mask manually

A region of interest (ROI) mask can be computed for instance with a statistical test. This requires a chain of image operations on the input data. Here is a possible recipe for computing an ROI mask:

  • Smoothing: Before a statistical test, it is often useful to smooth the image a bit using nilearn.image.smooth_img, typically fwhm=6 for fMRI.

  • Selecting voxels: Given the smoothed data, we can select voxels with a statistical test (eg opposing face and house experimental conditions), for instance with a simple Student’s t-test using scipy function scipy.stats.ttest_ind.

  • Thresholding: Then we need threshold the statistical map to have better representation of voxels of interest.

  • Mask intersection and dilation: Post-processing the results with simple morphological operations, mask intersection and dilation.

    • we can use another mask, such as a grey-matter mask, to select only the voxels which are common in both masks.

    • we can do morphological dilation to achieve more compact blobs with more regular boundaries. The function is used from scipy.ndimage.binary_dilation.

  • Extracting connected components: We end with splitting the connected ROIs into two separate regions (ROIs), one in each hemisphere. The function scipy.ndimage.label from the scipy library is used.

  • Saving the result: The final voxel mask is saved to disk using the ‘to_filename’ method of the image object. (or nibabel.save).

See also

For extracting connected components:

See also