Statistical testing of a second-level analysis

Perform a one-sample t-test on a bunch of images (a.k.a. second-level analysis in fMRI) and threshold the resulting statistical map.

This example is based on the so-called localizer dataset. It shows activation related to a mental computation task, as opposed to narrative sentence reading/listening.

Prepare some images for a simple t test

This is a simple manually performed second level analysis.

from nilearn import datasets

n_samples = 20
localizer_dataset = datasets.fetch_localizer_calculation_task(
    n_subjects=n_samples, legacy_format=False
)

[get_dataset_dir] Dataset found in
/home/runner/nilearn_data/brainomics_localizer
[fetch_single_file] Downloading data from
https://osf.io/download/5d27cbbd45253a00193c9b70/ ...
[fetch_single_file]  ...done. (3 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d27dbce45253a001a3c32fd/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d27e0221c5b4a001b9efb25/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d27ed481c5b4a001aa09e83/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28000845253a001c3e507a/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d281a2a45253a001c3e684c/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d282aa5114a42001605db5a/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28335545253a00193ce806/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28453a1c5b4a001c9ecaed/ ...
[fetch_single_file]  ...done. (3 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d284daf1c5b4a001d9fc4e5/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d2866c0a26b340017088827/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28781945253a00193d1237/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d2889a7a26b3400160a368f/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d288fb11c5b4a001d9ff738/ ...
[fetch_single_file]  ...done. (4 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28a4c0114a420016064fa2/ ...
[fetch_single_file]  ...done. (3 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28b6171c5b4a001c9f2ebd/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28d2bb114a420017054715/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28e056a26b340019093c95/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28e50945253a00193d6e09/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

[fetch_single_file] Downloading data from
https://osf.io/download/5d28ff54114a42001705610c/ ...
[fetch_single_file]  ...done. (2 seconds, 0 min)

Get the set of individual statstical maps (contrast estimates)

cmap_filenames = localizer_dataset.cmaps

Perform the second level analysis

First, we define a design matrix for the model. As the model is trivial (one-sample test), the design matrix is just one column with ones.

import pandas as pd

design_matrix = pd.DataFrame([1] * n_samples, columns=["intercept"])

Next, we specify and estimate the model.

from nilearn.glm.second_level import SecondLevelModel

second_level_model = SecondLevelModel(n_jobs=2).fit(
    cmap_filenames, design_matrix=design_matrix
)

Compute the only possible contrast: the one-sample test. Since there is only one possible contrast, we don’t need to specify it in detail.

z_map = second_level_model.compute_contrast(output_type="z_score")

Threshold the resulting map without multiple comparisons correction, abs(z) > 3.29 (equivalent to p < 0.001), cluster size > 10 voxels.

from nilearn.image import threshold_img

threshold_img(
    z_map,
    threshold=3.29,
    cluster_threshold=10,
    two_sided=True,
    copy_header=True,
)

<nibabel.nifti1.Nifti1Image object at 0x7f51b2224820>

This is equivalent to thresholding a z-statistic image with a false positive rate < .001, cluster size > 10 voxels.

from nilearn.glm import threshold_stats_img

thresholded_map1, threshold1 = threshold_stats_img(
    z_map,
    alpha=0.001,
    height_control="fpr",
    cluster_threshold=10,
    two_sided=True,
)

Now use FDR <.05 (False Discovery Rate) and no cluster-level threshold.

thresholded_map2, threshold2 = threshold_stats_img(
    z_map, alpha=0.05, height_control="fdr"
)
print(f"The FDR=.05 threshold is {threshold2:.3g}")

The FDR=.05 threshold is 2.37

Now use FWER <.05 (Family-Wise Error Rate) and no cluster-level threshold. As the data has not been intensively smoothed, we can use a simple Bonferroni correction.

thresholded_map3, threshold3 = threshold_stats_img(
    z_map, alpha=0.05, height_control="bonferroni"
)
print(f"The p<.05 Bonferroni-corrected threshold is {threshold3:.3g}")

The p<.05 Bonferroni-corrected threshold is 4.88

Visualize the results

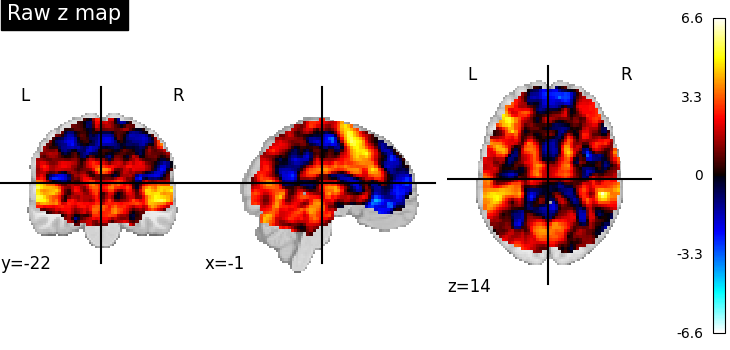
First, the unthresholded map.

from nilearn import plotting

display = plotting.plot_stat_map(z_map, title="Raw z map")

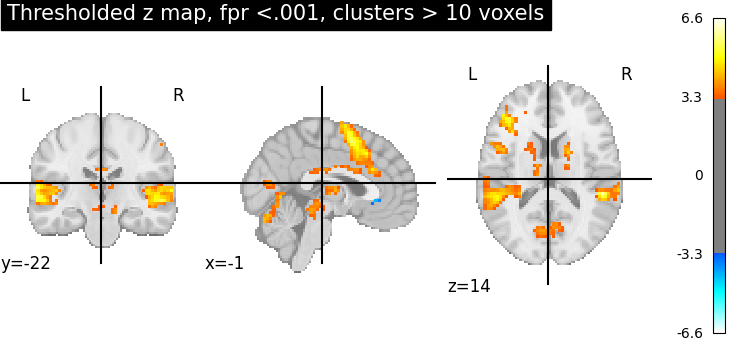
Second, the p<.001 uncorrected-thresholded map (with only clusters > 10 voxels).

plotting.plot_stat_map(
    thresholded_map1,
    cut_coords=display.cut_coords,
    threshold=threshold1,
    title="Thresholded z map, fpr <.001, clusters > 10 voxels",
)

<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f51b19ea520>

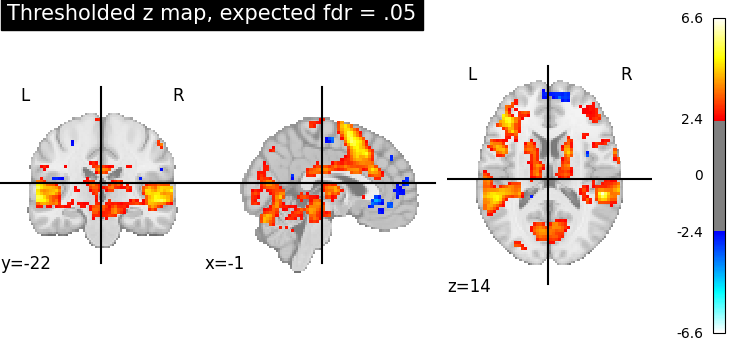
Third, the fdr-thresholded map.

plotting.plot_stat_map(
    thresholded_map2,
    cut_coords=display.cut_coords,
    title="Thresholded z map, expected fdr = .05",
    threshold=threshold2,
)

<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f51b145e3a0>

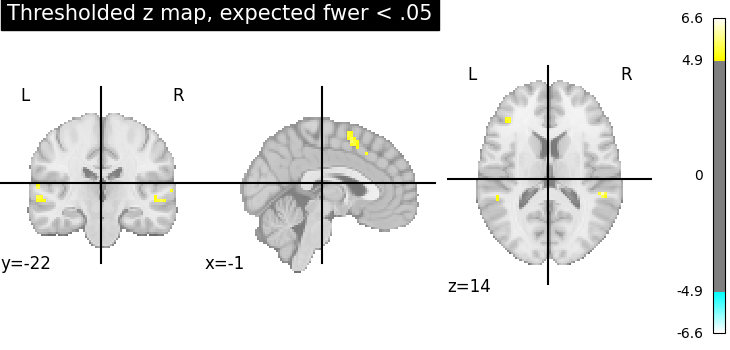
Fourth, the Bonferroni-thresholded map.

plotting.plot_stat_map(
    thresholded_map3,
    cut_coords=display.cut_coords,
    title="Thresholded z map, expected fwer < .05",
    threshold=threshold3,
)

<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7f519a2a5a60>

These different thresholds correspond to different statistical guarantees: in the FWER-corrected image there is only a probability smaller than .05 of observing any false positive voxel. In the FDR-corrected image, 5% of the voxels found are likely to be false positive. In the uncorrected image, one expects a few tens of false positive voxels.

plotting.show()

Estimated memory usage: 147 MB