Note
Go to the end to download the full example code or to run this example in your browser via Binder.
Voxel-Based Morphometry on Oasis dataset¶
This example uses Voxel-Based Morphometry (VBM) to study the relationship between aging and gray matter density.
The data come from the OASIS project. If you use it, you need to agree with the data usage agreement available on the website.
It has been run through a standard VBM pipeline (using SPM8 and NewSegment) to create VBM maps, which we study here.
Predictive modeling analysis: VBM bio-markers of aging?¶
We run a standard SVM-ANOVA nilearn pipeline to predict age from the VBM data. We use only 100 subjects from the OASIS dataset to limit the memory usage.
Note that for an actual predictive modeling study of aging, the study should be ran on the full set of subjects. Also, all parameters should be set by cross-validation. This includes the smoothing applied to the data and the number of features selected by the ANOVA step. Indeed, even these data-preparation parameter impact significantly the prediction score.
Also, parameters such as the smoothing should be applied to the data and the number of features selected by the ANOVA step should be set by nested cross-validation, as they impact significantly the prediction score.
Brain mapping with mass univariate¶
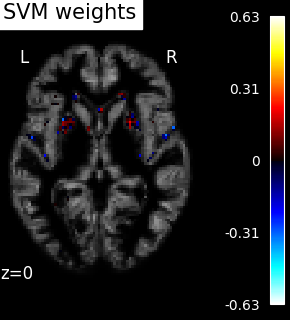
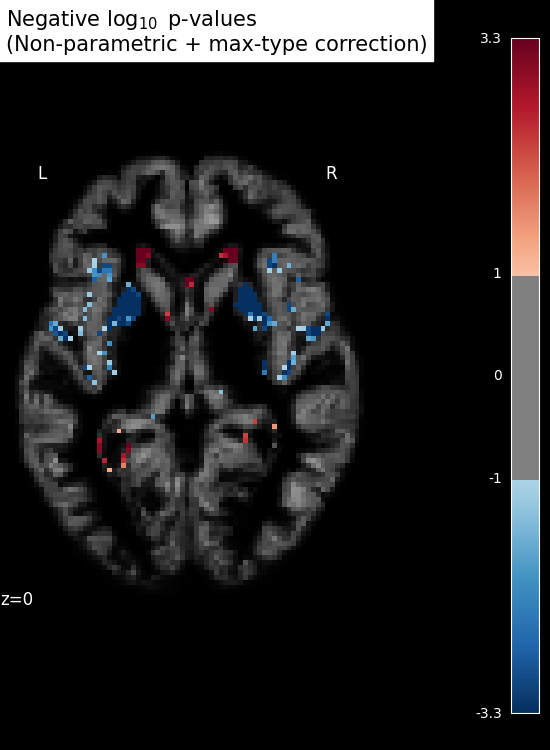
SVM weights are very noisy, partly because heavy smoothing is detrimental for the prediction here. A standard analysis using mass-univariate GLM (here permuted to have exact correction for multiple comparisons) gives a much clearer view of the important regions.
See also
For more information see the dataset description.
Warning
If you are using Nilearn with a version older than 0.9.0,
then you should either upgrade your version or import maskers
from the input_data module instead of the maskers module.
That is, you should manually replace in the following example all occurrences of:
from nilearn.maskers import NiftiMasker
with:
from nilearn.input_data import NiftiMasker
import numpy as np
from nilearn.datasets import fetch_oasis_vbm
from nilearn.image import get_data
from nilearn.maskers import NiftiMasker
n_subjects = 200 # more subjects requires more memory
Load Oasis dataset¶
oasis_dataset = fetch_oasis_vbm(n_subjects=n_subjects)
gray_matter_map_filenames = oasis_dataset.gray_matter_maps
age = oasis_dataset.ext_vars["age"].to_numpy()
# Split data into training set and test set
from sklearn.model_selection import train_test_split
gm_imgs_train, gm_imgs_test, age_train, age_test = train_test_split(
gray_matter_map_filenames, age, train_size=0.6, random_state=0
)
# print basic information on the dataset
print(
"First gray-matter anatomy image (3D) is located at: "
f"{oasis_dataset.gray_matter_maps[0]}"
)
print(
"First white-matter anatomy image (3D) is located at: "
f"{oasis_dataset.white_matter_maps[0]}"
)
[fetch_oasis_vbm] Dataset found in /home/runner/nilearn_data/oasis1
First gray-matter anatomy image (3D) is located at: /home/runner/nilearn_data/oasis1/OAS1_0001_MR1/mwrc1OAS1_0001_MR1_mpr_anon_fslswapdim_bet.nii.gz
First white-matter anatomy image (3D) is located at: /home/runner/nilearn_data/oasis1/OAS1_0001_MR1/mwrc2OAS1_0001_MR1_mpr_anon_fslswapdim_bet.nii.gz
Preprocess data¶
nifti_masker = NiftiMasker(
standardize=False, smoothing_fwhm=2, memory="nilearn_cache", verbose=1
) # cache options
gm_maps_masked = nifti_masker.fit_transform(gm_imgs_train)
# The features with too low between-subject variance are removed using
# :class:`sklearn.feature_selection.VarianceThreshold`.
from sklearn.feature_selection import VarianceThreshold
variance_threshold = VarianceThreshold(threshold=0.01)
variance_threshold.fit_transform(gm_maps_masked)
# Then we convert the data back to the mask image in order to use it for
# decoding process
mask = nifti_masker.inverse_transform(variance_threshold.get_support())
[NiftiMasker.wrapped] Loading data from
['/home/runner/nilearn_data/oasis1/OAS1_0211_MR1/mwrc1OAS1_0211_MR1_mpr_anon_fsl
swapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0052_MR1/mwrc1OAS1_0052_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0155_MR1/mwrc1OAS1_0155_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0221_MR1/mwrc1OAS1_0221_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0121_MR1/mwrc1OAS1_0121_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0070_MR1/mwrc1OAS1_0070_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0003_MR1/mwrc1OAS1_0003_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0067_MR1/mwrc1OAS1_0067_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0152_MR1/mwrc1OAS1_0152_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0224_MR1/mwrc1OAS1_0224_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0049_MR1/mwrc1OAS1_0049_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0012_MR1/mwrc1OAS1_0012_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0220_MR1/mwrc1OAS1_0220_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0081_MR1/mwrc1OAS1_0081_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0223_MR1/mwrc1OAS1_0223_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0202_MR1/mwrc1OAS1_0202_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0199_MR1/mwrc1OAS1_0199_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0141_MR1/mwrc1OAS1_0141_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0105_MR1/mwrc1OAS1_0105_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0126_MR1/mwrc1OAS1_0126_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0179_MR1/mwrc1OAS1_0179_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0216_MR1/mwrc1OAS1_0216_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0056_MR1/mwrc1OAS1_0056_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0001_MR1/mwrc1OAS1_0001_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0106_MR1/mwrc1OAS1_0106_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0124_MR1/mwrc1OAS1_0124_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0107_MR1/mwrc1OAS1_0107_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0072_MR1/mwrc1OAS1_0072_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0189_MR1/mwrc1OAS1_0189_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0046_MR1/mwrc1OAS1_0046_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0077_MR1/mwrc1OAS1_0077_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0055_MR1/mwrc1OAS1_0055_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0054_MR1/mwrc1OAS1_0054_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0096_MR1/mwrc1OAS1_0096_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0015_MR1/mwrc1OAS1_0015_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0182_MR1/mwrc1OAS1_0182_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0026_MR1/mwrc1OAS1_0026_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0210_MR1/mwrc1OAS1_0210_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0151_MR1/mwrc1OAS1_0151_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0022_MR1/mwrc1OAS1_0022_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0017_MR1/mwrc1OAS1_0017_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0087_MR1/mwrc1OAS1_0087_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0116_MR1/mwrc1OAS1_0116_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0059_MR1/mwrc1OAS1_0059_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0112_MR1/mwrc1OAS1_0112_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0085_MR1/mwrc1OAS1_0085_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0004_MR1/mwrc1OAS1_0004_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0131_MR1/mwrc1OAS1_0131_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0185_MR1/mwrc1OAS1_0185_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0226_MR1/mwrc1OAS1_0226_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0007_MR1/mwrc1OAS1_0007_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0076_MR1/mwrc1OAS1_0076_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0095_MR1/mwrc1OAS1_0095_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0136_MR1/mwrc1OAS1_0136_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0176_MR1/mwrc1OAS1_0176_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0193_MR1/mwrc1OAS1_0193_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0177_MR1/mwrc1OAS1_0177_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0103_MR1/mwrc1OAS1_0103_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0227_MR1/mwrc1OAS1_0227_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0013_MR1/mwrc1OAS1_0013_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0134_MR1/mwrc1OAS1_0134_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0114_MR1/mwrc1OAS1_0114_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0040_MR1/mwrc1OAS1_0040_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0064_MR1/mwrc1OAS1_0064_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0073_MR1/mwrc1OAS1_0073_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0002_MR1/mwrc1OAS1_0002_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0135_MR1/mwrc1OAS1_0135_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0183_MR1/mwrc1OAS1_0183_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0047_MR1/mwrc1OAS1_0047_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0117_MR1/mwrc1OAS1_0117_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0147_MR1/mwrc1OAS1_0147_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0197_MR1/mwrc1OAS1_0197_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0019_MR1/mwrc1OAS1_0019_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0043_MR1/mwrc1OAS1_0043_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0148_MR1/mwrc1OAS1_0148_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0060_MR1/mwrc1OAS1_0060_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0178_MR1/mwrc1OAS1_0178_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0143_MR1/mwrc1OAS1_0143_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0039_MR1/mwrc1OAS1_0039_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0032_MR1/mwrc1OAS1_0032_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0129_MR1/mwrc1OAS1_0129_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0169_MR1/mwrc1OAS1_0169_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0035_MR1/mwrc1OAS1_0035_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0188_MR1/mwrc1OAS1_0188_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0142_MR1/mwrc1OAS1_0142_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0200_MR1/mwrc1OAS1_0200_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0037_MR1/mwrc1OAS1_0037_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0160_MR1/mwrc1OAS1_0160_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0191_MR1/mwrc1OAS1_0191_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0165_MR1/mwrc1OAS1_0165_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0033_MR1/mwrc1OAS1_0033_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0111_MR1/mwrc1OAS1_0111_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0092_MR1/mwrc1OAS1_0092_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0088_MR1/mwrc1OAS1_0088_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0130_MR1/mwrc1OAS1_0130_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0166_MR1/mwrc1OAS1_0166_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0218_MR1/mwrc1OAS1_0218_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0080_MR1/mwrc1OAS1_0080_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0086_MR1/mwrc1OAS1_0086_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0029_MR1/mwrc1OAS1_0029_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0186_MR1/mwrc1OAS1_0186_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0091_MR1/mwrc1OAS1_0091_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0212_MR1/mwrc1OAS1_0212_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0198_MR1/mwrc1OAS1_0198_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0214_MR1/mwrc1OAS1_0214_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0044_MR1/mwrc1OAS1_0044_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0065_MR1/mwrc1OAS1_0065_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0158_MR1/mwrc1OAS1_0158_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0099_MR1/mwrc1OAS1_0099_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0078_MR1/mwrc1OAS1_0078_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0098_MR1/mwrc1OAS1_0098_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0041_MR1/mwrc1OAS1_0041_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0023_MR1/mwrc1OAS1_0023_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0011_MR1/mwrc1OAS1_0011_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0115_MR1/mwrc1OAS1_0115_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0075_MR1/mwrc1OAS1_0075_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0217_MR1/mwrc1OAS1_0217_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0132_MR1/mwrc1OAS1_0132_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0053_MR1/mwrc1OAS1_0053_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0195_MR1/mwrc1OAS1_0195_MR1_mpr_anon_fsls
wapdim_bet.nii.gz']
[NiftiMasker.wrapped] Computing mask
________________________________________________________________________________
[Memory] Calling nilearn.masking.compute_background_mask...
compute_background_mask([ '/home/runner/nilearn_data/oasis1/OAS1_0211_MR1/mwrc1OAS1_0211_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0052_MR1/mwrc1OAS1_0052_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0155_MR1/mwrc1OAS1_0155_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0221_MR1/mwrc1OAS1_0221_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0121_MR1/mwrc1OAS1_0121_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0070_MR1/mwrc1OAS1_0070_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0003_MR1/mwrc1OAS1_0003_MR1_mpr_anon_fslswapdim..., verbose=0)
__________________________________________compute_background_mask - 3.3s, 0.1min
[NiftiMasker.wrapped] Resampling mask
________________________________________________________________________________
[Memory] Calling nilearn.image.resampling.resample_img...
resample_img(<nibabel.nifti1.Nifti1Image object at 0x7f30b6a28b80>, target_affine=None, target_shape=None, copy=False, interpolation='nearest')
_____________________________________________________resample_img - 0.0s, 0.0min
[NiftiMasker.wrapped] Finished fit
________________________________________________________________________________
[Memory] Calling nilearn.maskers.nifti_masker.filter_and_mask...
filter_and_mask([ '/home/runner/nilearn_data/oasis1/OAS1_0211_MR1/mwrc1OAS1_0211_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0052_MR1/mwrc1OAS1_0052_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0155_MR1/mwrc1OAS1_0155_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0221_MR1/mwrc1OAS1_0221_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0121_MR1/mwrc1OAS1_0121_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0070_MR1/mwrc1OAS1_0070_MR1_mpr_anon_fslswapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0003_MR1/mwrc1OAS1_0003_MR1_mpr_anon_fslswapdim...,
<nibabel.nifti1.Nifti1Image object at 0x7f30b6a28b80>, { 'clean_args': None,
'clean_kwargs': {},
'cmap': 'gray',
'detrend': False,
'dtype': None,
'high_pass': None,
'high_variance_confounds': False,
'low_pass': None,
'reports': True,
'runs': None,
'smoothing_fwhm': 2,
'standardize': False,
'standardize_confounds': True,
't_r': None,
'target_affine': None,
'target_shape': None}, memory_level=1, memory=Memory(location=nilearn_cache/joblib), verbose=1, confounds=None, sample_mask=None, copy=True, dtype=None, sklearn_output_config=None)
[NiftiMasker.wrapped] Loading data from <nibabel.nifti1.Nifti1Image object at
0x7f30a30a9d20>
[NiftiMasker.wrapped] Smoothing images
[NiftiMasker.wrapped] Extracting region signals
[NiftiMasker.wrapped] Cleaning extracted signals
_________________________________________________filter_and_mask - 10.0s, 0.2min
[NiftiMasker.inverse_transform] Computing image from signals
________________________________________________________________________________
[Memory] Calling nilearn.masking.unmask...
unmask(array([False, ..., False], shape=(902629,)), <nibabel.nifti1.Nifti1Image object at 0x7f30b6a28b80>)
___________________________________________________________unmask - 0.3s, 0.0min
Prediction pipeline with ANOVA and SVR using
DecoderRegressor Object
In nilearn we can benefit from the built-in DecoderRegressor object to
do ANOVA with SVR instead of manually defining the whole pipeline.
This estimator also uses Cross Validation to select best models and ensemble
them. Furthermore, you can pass n_jobs=<some_high_value> to the
DecoderRegressor class to take advantage of a multi-core system.
To save time (because these are anat images with many voxels), we include
only the 1-percent voxels most correlated with the age variable to fit. We
also want to set mask hyperparameter to be the mask we just obtained above.
from nilearn.decoding import DecoderRegressor
decoder = DecoderRegressor(
estimator="svr",
mask=mask,
scoring="neg_mean_absolute_error",
screening_percentile=1,
n_jobs=2,
standardize="zscore_sample",
verbose=1,
)
# Fit and predict with the decoder
decoder.fit(gm_imgs_train, age_train)
# Sort test data for better visualization (trend, etc.)
perm = np.argsort(age_test)[::-1]
age_test = age_test[perm]
gm_imgs_test = np.array(gm_imgs_test)[perm]
age_pred = decoder.predict(gm_imgs_test)
prediction_score = -np.mean(decoder.cv_scores_["beta"])
print("=== DECODER ===")
print(f"explained variance for the cross-validation: {prediction_score:f}")
print()
[DecoderRegressor.fit] Loading data from
['/home/runner/nilearn_data/oasis1/OAS1_0211_MR1/mwrc1OAS1_0211_MR1_mpr_anon_fsl
swapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0052_MR1/mwrc1OAS1_0052_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0155_MR1/mwrc1OAS1_0155_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0221_MR1/mwrc1OAS1_0221_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0121_MR1/mwrc1OAS1_0121_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0070_MR1/mwrc1OAS1_0070_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0003_MR1/mwrc1OAS1_0003_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0067_MR1/mwrc1OAS1_0067_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0152_MR1/mwrc1OAS1_0152_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0224_MR1/mwrc1OAS1_0224_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0049_MR1/mwrc1OAS1_0049_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0012_MR1/mwrc1OAS1_0012_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0220_MR1/mwrc1OAS1_0220_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0081_MR1/mwrc1OAS1_0081_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0223_MR1/mwrc1OAS1_0223_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0202_MR1/mwrc1OAS1_0202_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0199_MR1/mwrc1OAS1_0199_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0141_MR1/mwrc1OAS1_0141_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0105_MR1/mwrc1OAS1_0105_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0126_MR1/mwrc1OAS1_0126_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0179_MR1/mwrc1OAS1_0179_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0216_MR1/mwrc1OAS1_0216_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0056_MR1/mwrc1OAS1_0056_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0001_MR1/mwrc1OAS1_0001_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0106_MR1/mwrc1OAS1_0106_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0124_MR1/mwrc1OAS1_0124_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0107_MR1/mwrc1OAS1_0107_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0072_MR1/mwrc1OAS1_0072_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0189_MR1/mwrc1OAS1_0189_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0046_MR1/mwrc1OAS1_0046_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0077_MR1/mwrc1OAS1_0077_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0055_MR1/mwrc1OAS1_0055_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0054_MR1/mwrc1OAS1_0054_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0096_MR1/mwrc1OAS1_0096_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0015_MR1/mwrc1OAS1_0015_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0182_MR1/mwrc1OAS1_0182_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0026_MR1/mwrc1OAS1_0026_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0210_MR1/mwrc1OAS1_0210_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0151_MR1/mwrc1OAS1_0151_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0022_MR1/mwrc1OAS1_0022_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0017_MR1/mwrc1OAS1_0017_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0087_MR1/mwrc1OAS1_0087_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0116_MR1/mwrc1OAS1_0116_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0059_MR1/mwrc1OAS1_0059_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0112_MR1/mwrc1OAS1_0112_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0085_MR1/mwrc1OAS1_0085_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0004_MR1/mwrc1OAS1_0004_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0131_MR1/mwrc1OAS1_0131_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0185_MR1/mwrc1OAS1_0185_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0226_MR1/mwrc1OAS1_0226_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0007_MR1/mwrc1OAS1_0007_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0076_MR1/mwrc1OAS1_0076_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0095_MR1/mwrc1OAS1_0095_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0136_MR1/mwrc1OAS1_0136_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0176_MR1/mwrc1OAS1_0176_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0193_MR1/mwrc1OAS1_0193_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0177_MR1/mwrc1OAS1_0177_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0103_MR1/mwrc1OAS1_0103_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0227_MR1/mwrc1OAS1_0227_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0013_MR1/mwrc1OAS1_0013_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0134_MR1/mwrc1OAS1_0134_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0114_MR1/mwrc1OAS1_0114_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0040_MR1/mwrc1OAS1_0040_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0064_MR1/mwrc1OAS1_0064_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0073_MR1/mwrc1OAS1_0073_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0002_MR1/mwrc1OAS1_0002_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0135_MR1/mwrc1OAS1_0135_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0183_MR1/mwrc1OAS1_0183_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0047_MR1/mwrc1OAS1_0047_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0117_MR1/mwrc1OAS1_0117_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0147_MR1/mwrc1OAS1_0147_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0197_MR1/mwrc1OAS1_0197_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0019_MR1/mwrc1OAS1_0019_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0043_MR1/mwrc1OAS1_0043_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0148_MR1/mwrc1OAS1_0148_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0060_MR1/mwrc1OAS1_0060_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0178_MR1/mwrc1OAS1_0178_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0143_MR1/mwrc1OAS1_0143_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0039_MR1/mwrc1OAS1_0039_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0032_MR1/mwrc1OAS1_0032_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0129_MR1/mwrc1OAS1_0129_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0169_MR1/mwrc1OAS1_0169_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0035_MR1/mwrc1OAS1_0035_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0188_MR1/mwrc1OAS1_0188_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0142_MR1/mwrc1OAS1_0142_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0200_MR1/mwrc1OAS1_0200_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0037_MR1/mwrc1OAS1_0037_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0160_MR1/mwrc1OAS1_0160_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0191_MR1/mwrc1OAS1_0191_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0165_MR1/mwrc1OAS1_0165_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0033_MR1/mwrc1OAS1_0033_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0111_MR1/mwrc1OAS1_0111_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0092_MR1/mwrc1OAS1_0092_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0088_MR1/mwrc1OAS1_0088_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0130_MR1/mwrc1OAS1_0130_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0166_MR1/mwrc1OAS1_0166_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0218_MR1/mwrc1OAS1_0218_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0080_MR1/mwrc1OAS1_0080_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0086_MR1/mwrc1OAS1_0086_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0029_MR1/mwrc1OAS1_0029_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0186_MR1/mwrc1OAS1_0186_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0091_MR1/mwrc1OAS1_0091_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0212_MR1/mwrc1OAS1_0212_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0198_MR1/mwrc1OAS1_0198_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0214_MR1/mwrc1OAS1_0214_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0044_MR1/mwrc1OAS1_0044_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0065_MR1/mwrc1OAS1_0065_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0158_MR1/mwrc1OAS1_0158_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0099_MR1/mwrc1OAS1_0099_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0078_MR1/mwrc1OAS1_0078_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0098_MR1/mwrc1OAS1_0098_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0041_MR1/mwrc1OAS1_0041_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0023_MR1/mwrc1OAS1_0023_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0011_MR1/mwrc1OAS1_0011_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0115_MR1/mwrc1OAS1_0115_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0075_MR1/mwrc1OAS1_0075_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0217_MR1/mwrc1OAS1_0217_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0132_MR1/mwrc1OAS1_0132_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0053_MR1/mwrc1OAS1_0053_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0195_MR1/mwrc1OAS1_0195_MR1_mpr_anon_fsls
wapdim_bet.nii.gz']
[DecoderRegressor.fit] Loading mask from <nibabel.nifti1.Nifti1Image object at
0x7f30b6a29420>
/home/runner/work/nilearn/nilearn/examples/02_decoding/plot_oasis_vbm.py:129: UserWarning: [NiftiMasker.fit] Generation of a mask has been requested (imgs != None) while a mask was given at masker creation. Given mask will be used.
decoder.fit(gm_imgs_train, age_train)
[DecoderRegressor.fit] Resampling mask
[DecoderRegressor.fit] Finished fit
[DecoderRegressor.fit] Loading data from <nibabel.nifti1.Nifti1Image object at
0x7f30a30e13f0>
[DecoderRegressor.fit] Extracting region signals
[DecoderRegressor.fit] Cleaning extracted signals
[DecoderRegressor.fit] Mask volume = 1.21634e+06mm^3 = 1216.34cm^3
[DecoderRegressor.fit] Standard brain volume = 1.88299e+06mm^3
[DecoderRegressor.fit] Original screening-percentile: 1
[DecoderRegressor.fit] Corrected screening-percentile: 1.54807
[Parallel(n_jobs=2)]: Using backend LokyBackend with 2 concurrent workers.
[Parallel(n_jobs=2)]: Done 10 out of 10 | elapsed: 3.8s finished
[DecoderRegressor.fit] Computing image from signals
[DecoderRegressor.fit] Computing image from signals
[DecoderRegressor.predict] Loading data from <nibabel.nifti1.Nifti1Image object
at 0x7f30b6a2b970>
[DecoderRegressor.predict] Extracting region signals
[DecoderRegressor.predict] Cleaning extracted signals
=== DECODER ===
explained variance for the cross-validation: 11.774939
Visualization¶
weight_img = decoder.coef_img_["beta"]
# Create the figure
from nilearn.plotting import plot_stat_map, show
bg_filename = gray_matter_map_filenames[0]
z_slice = 0
display = plot_stat_map(
weight_img,
bg_img=bg_filename,
display_mode="z",
cut_coords=[z_slice],
title="SVM weights",
)
show()
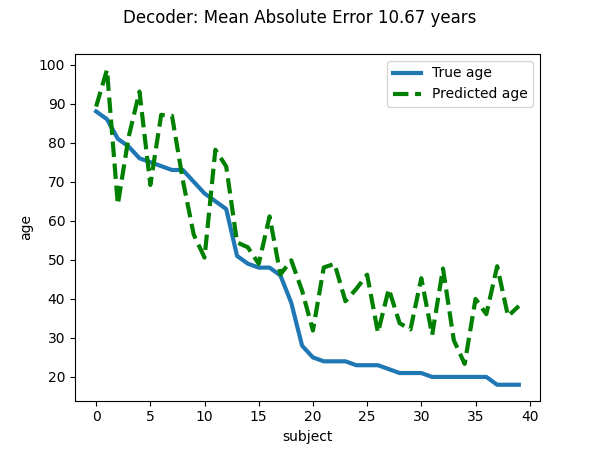
Visualize the quality of predictions¶
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 4.5))
plt.suptitle(f"Decoder: Mean Absolute Error {prediction_score:.2f} years")
linewidth = 3
plt.plot(age_test, label="True age", linewidth=linewidth)
plt.plot(age_pred, "--", c="g", label="Predicted age", linewidth=linewidth)
plt.ylabel("age")
plt.xlabel("subject")
plt.legend(loc="best")
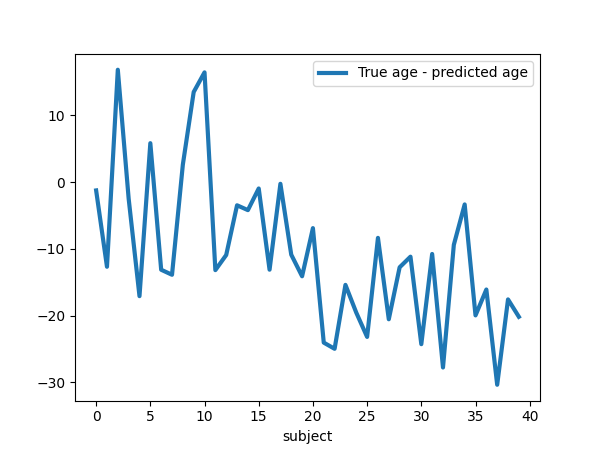
plt.figure(figsize=(6, 4.5))
plt.plot(
age_test - age_pred, label="True age - predicted age", linewidth=linewidth
)
plt.xlabel("subject")
plt.legend(loc="best")
<matplotlib.legend.Legend object at 0x7f30a2b04220>
Inference with massively univariate model¶
print("Massively univariate model")
gm_maps_masked = NiftiMasker(verbose=1).fit_transform(
gray_matter_map_filenames
)
data = variance_threshold.fit_transform(gm_maps_masked)
# Statistical inference
from nilearn.mass_univariate import permuted_ols
# This can be changed to use more CPUs.
output = permuted_ols(
age,
data, # + intercept as a covariate by default
n_perm=2000, # 1,000 in the interest of time; 10000 would be better
verbose=1, # display progress bar
n_jobs=2,
)
neg_log_pvals = output["logp_max_t"]
t_scores_original_data = output["t"]
signed_neg_log_pvals = neg_log_pvals * np.sign(t_scores_original_data)
signed_neg_log_pvals_unmasked = nifti_masker.inverse_transform(
variance_threshold.inverse_transform(signed_neg_log_pvals)
)
# Show results
threshold = -np.log10(0.1) # 10% corrected
n_detections = (get_data(signed_neg_log_pvals_unmasked) > threshold).sum()
title = (
"Negative $\\log_{10}$ p-values\n(Non-parametric + max-type correction)"
f"\n{int(n_detections)} detections"
)
plot_stat_map(
signed_neg_log_pvals_unmasked,
bg_img=bg_filename,
threshold=threshold,
display_mode="z",
cut_coords=[z_slice],
figure=plt.figure(figsize=(5.5, 7.5), facecolor="k"),
title=title,
)
show()
Massively univariate model
[NiftiMasker.wrapped] Loading data from
['/home/runner/nilearn_data/oasis1/OAS1_0001_MR1/mwrc1OAS1_0001_MR1_mpr_anon_fsl
swapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0002_MR1/mwrc1OAS1_0002_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0003_MR1/mwrc1OAS1_0003_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0004_MR1/mwrc1OAS1_0004_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0005_MR1/mwrc1OAS1_0005_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0006_MR1/mwrc1OAS1_0006_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0007_MR1/mwrc1OAS1_0007_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0009_MR1/mwrc1OAS1_0009_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0010_MR1/mwrc1OAS1_0010_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0011_MR1/mwrc1OAS1_0011_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0012_MR1/mwrc1OAS1_0012_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0013_MR1/mwrc1OAS1_0013_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0014_MR1/mwrc1OAS1_0014_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0015_MR1/mwrc1OAS1_0015_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0016_MR1/mwrc1OAS1_0016_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0017_MR1/mwrc1OAS1_0017_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0018_MR1/mwrc1OAS1_0018_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0019_MR1/mwrc1OAS1_0019_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0020_MR1/mwrc1OAS1_0020_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0021_MR1/mwrc1OAS1_0021_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0022_MR1/mwrc1OAS1_0022_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0023_MR1/mwrc1OAS1_0023_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0025_MR1/mwrc1OAS1_0025_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0026_MR1/mwrc1OAS1_0026_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0028_MR1/mwrc1OAS1_0028_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0029_MR1/mwrc1OAS1_0029_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0030_MR1/mwrc1OAS1_0030_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0031_MR1/mwrc1OAS1_0031_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0032_MR1/mwrc1OAS1_0032_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0033_MR1/mwrc1OAS1_0033_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0034_MR1/mwrc1OAS1_0034_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0035_MR1/mwrc1OAS1_0035_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0037_MR1/mwrc1OAS1_0037_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0038_MR1/mwrc1OAS1_0038_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0039_MR1/mwrc1OAS1_0039_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0040_MR1/mwrc1OAS1_0040_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0041_MR1/mwrc1OAS1_0041_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0042_MR1/mwrc1OAS1_0042_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0043_MR1/mwrc1OAS1_0043_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0044_MR1/mwrc1OAS1_0044_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0045_MR1/mwrc1OAS1_0045_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0046_MR1/mwrc1OAS1_0046_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0047_MR1/mwrc1OAS1_0047_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0049_MR1/mwrc1OAS1_0049_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0050_MR1/mwrc1OAS1_0050_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0051_MR1/mwrc1OAS1_0051_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0052_MR1/mwrc1OAS1_0052_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0053_MR1/mwrc1OAS1_0053_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0054_MR1/mwrc1OAS1_0054_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0055_MR1/mwrc1OAS1_0055_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0056_MR1/mwrc1OAS1_0056_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0058_MR1/mwrc1OAS1_0058_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0059_MR1/mwrc1OAS1_0059_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0060_MR1/mwrc1OAS1_0060_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0061_MR1/mwrc1OAS1_0061_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0062_MR1/mwrc1OAS1_0062_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0063_MR1/mwrc1OAS1_0063_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0064_MR1/mwrc1OAS1_0064_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0065_MR1/mwrc1OAS1_0065_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0067_MR1/mwrc1OAS1_0067_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0068_MR1/mwrc1OAS1_0068_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0069_MR1/mwrc1OAS1_0069_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0070_MR1/mwrc1OAS1_0070_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0071_MR1/mwrc1OAS1_0071_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0072_MR1/mwrc1OAS1_0072_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0073_MR1/mwrc1OAS1_0073_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0074_MR1/mwrc1OAS1_0074_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0075_MR1/mwrc1OAS1_0075_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0076_MR1/mwrc1OAS1_0076_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0077_MR1/mwrc1OAS1_0077_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0078_MR1/mwrc1OAS1_0078_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0079_MR1/mwrc1OAS1_0079_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0080_MR1/mwrc1OAS1_0080_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0081_MR1/mwrc1OAS1_0081_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0082_MR1/mwrc1OAS1_0082_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0084_MR1/mwrc1OAS1_0084_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0085_MR1/mwrc1OAS1_0085_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0086_MR1/mwrc1OAS1_0086_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0087_MR1/mwrc1OAS1_0087_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0088_MR1/mwrc1OAS1_0088_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0090_MR1/mwrc1OAS1_0090_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0091_MR1/mwrc1OAS1_0091_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0092_MR1/mwrc1OAS1_0092_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0094_MR1/mwrc1OAS1_0094_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0095_MR1/mwrc1OAS1_0095_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0096_MR1/mwrc1OAS1_0096_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0097_MR1/mwrc1OAS1_0097_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0098_MR1/mwrc1OAS1_0098_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0099_MR1/mwrc1OAS1_0099_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0101_MR1/mwrc1OAS1_0101_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0102_MR1/mwrc1OAS1_0102_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0103_MR1/mwrc1OAS1_0103_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0104_MR1/mwrc1OAS1_0104_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0105_MR1/mwrc1OAS1_0105_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0106_MR1/mwrc1OAS1_0106_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0107_MR1/mwrc1OAS1_0107_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0108_MR1/mwrc1OAS1_0108_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0109_MR1/mwrc1OAS1_0109_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0110_MR1/mwrc1OAS1_0110_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0111_MR1/mwrc1OAS1_0111_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0112_MR1/mwrc1OAS1_0112_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0113_MR1/mwrc1OAS1_0113_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0114_MR1/mwrc1OAS1_0114_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0115_MR1/mwrc1OAS1_0115_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0116_MR1/mwrc1OAS1_0116_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0117_MR1/mwrc1OAS1_0117_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0119_MR1/mwrc1OAS1_0119_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0120_MR1/mwrc1OAS1_0120_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0121_MR1/mwrc1OAS1_0121_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0123_MR1/mwrc1OAS1_0123_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0124_MR1/mwrc1OAS1_0124_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0125_MR1/mwrc1OAS1_0125_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0126_MR1/mwrc1OAS1_0126_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0127_MR1/mwrc1OAS1_0127_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0129_MR1/mwrc1OAS1_0129_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0130_MR1/mwrc1OAS1_0130_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0131_MR1/mwrc1OAS1_0131_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0132_MR1/mwrc1OAS1_0132_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0133_MR1/mwrc1OAS1_0133_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0134_MR1/mwrc1OAS1_0134_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0135_MR1/mwrc1OAS1_0135_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0136_MR1/mwrc1OAS1_0136_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0137_MR1/mwrc1OAS1_0137_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0138_MR1/mwrc1OAS1_0138_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0139_MR1/mwrc1OAS1_0139_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0140_MR1/mwrc1OAS1_0140_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0141_MR1/mwrc1OAS1_0141_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0142_MR1/mwrc1OAS1_0142_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0143_MR1/mwrc1OAS1_0143_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0144_MR1/mwrc1OAS1_0144_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0145_MR1/mwrc1OAS1_0145_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0146_MR1/mwrc1OAS1_0146_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0147_MR1/mwrc1OAS1_0147_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0148_MR1/mwrc1OAS1_0148_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0150_MR1/mwrc1OAS1_0150_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0151_MR1/mwrc1OAS1_0151_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0152_MR1/mwrc1OAS1_0152_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0153_MR1/mwrc1OAS1_0153_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0155_MR1/mwrc1OAS1_0155_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0156_MR1/mwrc1OAS1_0156_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0158_MR1/mwrc1OAS1_0158_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0159_MR1/mwrc1OAS1_0159_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0160_MR1/mwrc1OAS1_0160_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0161_MR1/mwrc1OAS1_0161_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0162_MR1/mwrc1OAS1_0162_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0163_MR1/mwrc1OAS1_0163_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0164_MR1/mwrc1OAS1_0164_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0165_MR1/mwrc1OAS1_0165_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0166_MR1/mwrc1OAS1_0166_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0167_MR1/mwrc1OAS1_0167_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0168_MR1/mwrc1OAS1_0168_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0169_MR1/mwrc1OAS1_0169_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0170_MR1/mwrc1OAS1_0170_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0173_MR1/mwrc1OAS1_0173_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0174_MR1/mwrc1OAS1_0174_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0176_MR1/mwrc1OAS1_0176_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0177_MR1/mwrc1OAS1_0177_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0178_MR1/mwrc1OAS1_0178_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0179_MR1/mwrc1OAS1_0179_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0180_MR1/mwrc1OAS1_0180_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0181_MR1/mwrc1OAS1_0181_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0182_MR1/mwrc1OAS1_0182_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0183_MR1/mwrc1OAS1_0183_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0184_MR1/mwrc1OAS1_0184_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0185_MR1/mwrc1OAS1_0185_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0186_MR1/mwrc1OAS1_0186_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0188_MR1/mwrc1OAS1_0188_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0189_MR1/mwrc1OAS1_0189_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0190_MR1/mwrc1OAS1_0190_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0191_MR1/mwrc1OAS1_0191_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0192_MR1/mwrc1OAS1_0192_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0193_MR1/mwrc1OAS1_0193_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0195_MR1/mwrc1OAS1_0195_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0197_MR1/mwrc1OAS1_0197_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0198_MR1/mwrc1OAS1_0198_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0199_MR1/mwrc1OAS1_0199_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0200_MR1/mwrc1OAS1_0200_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0201_MR1/mwrc1OAS1_0201_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0202_MR1/mwrc1OAS1_0202_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0203_MR1/mwrc1OAS1_0203_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0204_MR1/mwrc1OAS1_0204_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0205_MR1/mwrc1OAS1_0205_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0206_MR1/mwrc1OAS1_0206_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0207_MR1/mwrc1OAS1_0207_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0208_MR1/mwrc1OAS1_0208_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0209_MR1/mwrc1OAS1_0209_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0210_MR1/mwrc1OAS1_0210_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0211_MR1/mwrc1OAS1_0211_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0212_MR1/mwrc1OAS1_0212_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0213_MR1/mwrc1OAS1_0213_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0214_MR1/mwrc1OAS1_0214_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0216_MR1/mwrc1OAS1_0216_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0217_MR1/mwrc1OAS1_0217_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0218_MR1/mwrc1OAS1_0218_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0220_MR1/mwrc1OAS1_0220_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0221_MR1/mwrc1OAS1_0221_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0223_MR1/mwrc1OAS1_0223_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0224_MR1/mwrc1OAS1_0224_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0226_MR1/mwrc1OAS1_0226_MR1_mpr_anon_fsls
wapdim_bet.nii.gz',
'/home/runner/nilearn_data/oasis1/OAS1_0227_MR1/mwrc1OAS1_0227_MR1_mpr_anon_fsls
wapdim_bet.nii.gz']
[NiftiMasker.wrapped] Computing mask
[NiftiMasker.wrapped] Resampling mask
[NiftiMasker.wrapped] Finished fit
[NiftiMasker.wrapped] Loading data from <nibabel.nifti1.Nifti1Image object at
0x7f30a30fe890>
[NiftiMasker.wrapped] Extracting region signals
[NiftiMasker.wrapped] Cleaning extracted signals
[Parallel(n_jobs=2)]: Using backend LokyBackend with 2 concurrent workers.
[Parallel(n_jobs=2)]: Done 2 out of 2 | elapsed: 1.0min finished
[NiftiMasker.inverse_transform] Computing image from signals
________________________________________________________________________________
[Memory] Calling nilearn.masking.unmask...
unmask(array([[0., ..., 0.]], shape=(1, 902629)), <nibabel.nifti1.Nifti1Image object at 0x7f30b6a28b80>)
___________________________________________________________unmask - 0.3s, 0.0min
Total running time of the script: (2 minutes 18.398 seconds)
Estimated memory usage: 5260 MB