Massively univariate analysis of face vs house recognition

A permuted Ordinary Least Squares algorithm is run at each voxel in order to determine whether or not it behaves differently under a “face viewing” condition and a “house viewing” condition. We consider the mean image per run and per condition. Otherwise, the observations cannot be exchanged at random because a time dependence exists between observations within a same run (see Winkler et al.[1] for more detailed explanations).

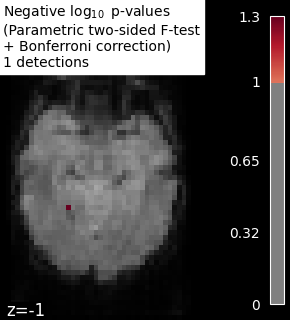
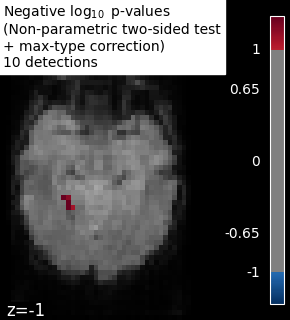
The example shows the small differences that exist between Bonferroni-corrected p-values and family-wise corrected p-values obtained from a permutation test combined with a max-type procedure (Anderson and Robinson[2]). Bonferroni correction is a bit conservative, as revealed by the presence of a few false negative.

Note

If you are using Nilearn with a version older than 0.9.0, then you should either upgrade your version or import maskers from the input_data module instead of the maskers module.

That is, you should manually replace in the following example all occurrences of:

from nilearn.maskers import NiftiMasker

with:

from nilearn.input_data import NiftiMasker

Load Haxby dataset

from nilearn import datasets, image
from nilearn.plotting import plot_stat_map, show

haxby_dataset = datasets.fetch_haxby(subjects=[2])

# print basic information on the dataset
print(f"Mask nifti image (3D) is located at: {haxby_dataset.mask}")
print(f"Functional nifti image (4D) is located at: {haxby_dataset.func[0]}")

[fetch_haxby] Dataset found in /home/runner/nilearn_data/haxby2001
Mask nifti image (3D) is located at: /home/runner/nilearn_data/haxby2001/mask.nii.gz
Functional nifti image (4D) is located at: /home/runner/nilearn_data/haxby2001/subj2/bold.nii.gz

Restrict to faces and houses

import numpy as np
import pandas as pd

labels = pd.read_csv(haxby_dataset.session_target[0], sep=" ")
conditions = labels["labels"]
categories = conditions.unique()
conditions_encoded = np.zeros_like(conditions)
for c, category in enumerate(categories):
    conditions_encoded[conditions == category] = c
runs = labels["chunks"]
condition_mask = conditions.isin(["face", "house"])
conditions_encoded = conditions_encoded[condition_mask]

Mask data

from nilearn.image import index_img
from nilearn.maskers import NiftiMasker

mask_filename = haxby_dataset.mask

nifti_masker = NiftiMasker(
    smoothing_fwhm=8,
    mask_img=mask_filename,
    memory="nilearn_cache",  # cache options
    memory_level=1,
)
func_filename = haxby_dataset.func[0]
func_reduced = index_img(func_filename, condition_mask)
fmri_masked = nifti_masker.fit_transform(func_reduced)

# We consider the mean image per run and per condition.
# Otherwise, the observations cannot be exchanged at random because
# a time dependence exists between observations within a same run.
n_runs = np.unique(runs).size
conditions_per_run = 2
grouped_fmri_masked = np.empty(
    (conditions_per_run * n_runs, fmri_masked.shape[1])
)
grouped_conditions_encoded = np.empty((conditions_per_run * n_runs, 1))

for s in range(n_runs):
    run_mask = runs[condition_mask] == s
    run_house_mask = np.logical_and(
        run_mask, conditions[condition_mask] == "house"
    )
    run_face_mask = np.logical_and(
        run_mask, conditions[condition_mask] == "face"
    )
    grouped_fmri_masked[2 * s] = fmri_masked[run_house_mask].mean(0)
    grouped_fmri_masked[2 * s + 1] = fmri_masked[run_face_mask].mean(0)
    grouped_conditions_encoded[2 * s] = conditions_encoded[run_house_mask][0]
    grouped_conditions_encoded[2 * s + 1] = conditions_encoded[run_face_mask][
        0
    ]

Perform massively univariate analysis with permuted OLS

We use a two-sided t-test to compute p-values, but we keep trace of the effect sign to add it back at the end and thus observe the signed effect

from nilearn.mass_univariate import permuted_ols

# Note that an intercept as a covariate is used by default
neg_log_pvals, t_scores_original_data, _ = permuted_ols(
    grouped_conditions_encoded,
    grouped_fmri_masked,
    n_perm=10000,
    two_sided_test=True,
    verbose=1,  # display progress bar
    n_jobs=2,  # can be changed to use more CPUs
)
signed_neg_log_pvals = neg_log_pvals * np.sign(t_scores_original_data)
signed_neg_log_pvals_unmasked = nifti_masker.inverse_transform(
    signed_neg_log_pvals
)

/home/runner/work/nilearn/nilearn/examples/07_advanced/plot_haxby_mass_univariate.py:103: DeprecationWarning: The "legacy" output structure for "permuted_ols" is deprecated. The default output structure will be changed to "dict" in version 0.13.
  neg_log_pvals, t_scores_original_data, _ = permuted_ols(
[Parallel(n_jobs=2)]: Using backend LokyBackend with 2 concurrent workers.
[Parallel(n_jobs=2)]: Done   2 out of   2 | elapsed:    6.8s remaining:    0.0s
[Parallel(n_jobs=2)]: Done   2 out of   2 | elapsed:    6.8s finished

scikit-learn F-scores for comparison

F-test does not allow to observe the effect sign (pure two-sided test)

from sklearn.feature_selection import f_regression

# f_regression implicitly adds intercept
_, pvals_bonferroni = f_regression(
    grouped_fmri_masked,
    grouped_conditions_encoded.ravel(),
)
pvals_bonferroni *= fmri_masked.shape[1]
pvals_bonferroni[np.isnan(pvals_bonferroni)] = 1
pvals_bonferroni[pvals_bonferroni > 1] = 1
neg_log_pvals_bonferroni = -np.log10(pvals_bonferroni)
neg_log_pvals_bonferroni_unmasked = nifti_masker.inverse_transform(
    neg_log_pvals_bonferroni
)

Visualization

from nilearn.image import get_data

# Use the fMRI mean image as a surrogate of anatomical data
mean_fmri_img = image.mean_img(func_filename, copy_header=True)

threshold = -np.log10(0.1)  # 10% corrected

vmax = min(signed_neg_log_pvals.max(), neg_log_pvals_bonferroni.max())

# Plot thresholded p-values map corresponding to F-scores

neg_log_pvals_bonferroni_data = get_data(neg_log_pvals_bonferroni_unmasked)
n_detections = (neg_log_pvals_bonferroni_data > threshold).sum()
title = (
    "Negative $\\log_{10}$ p-values"
    "\n(Parametric two-sided F-test"
    "\n+ Bonferroni correction)"
    f"\n{n_detections} detections"
)

display = plot_stat_map(
    neg_log_pvals_bonferroni_unmasked,
    mean_fmri_img,
    threshold=threshold,
    display_mode="z",
    cut_coords=[-1],
    vmax=vmax,
    vmin=threshold,
    cmap="inferno",
)

display.title(title, size=10)

# Plot permutation p-values map
n_detections = (np.abs(signed_neg_log_pvals) > threshold).sum()
title = (
    "Negative $\\log_{10}$ p-values"
    "\n(Non-parametric two-sided test"
    "\n+ max-type correction)"
    f"\n{n_detections} detections"
)

display = plot_stat_map(
    signed_neg_log_pvals_unmasked,
    mean_fmri_img,
    threshold=threshold,
    display_mode="z",
    cut_coords=[-1],
    vmax=vmax,
    vmin=threshold,
    cmap="inferno",
)

display.title(title, size=10)

show()

• 
• 

/home/runner/work/nilearn/nilearn/.tox/doc/lib/python3.9/site-packages/nilearn/plotting/displays/_slicers.py:1666: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance.  In a future version, a new instance will always be created and returned.  Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.
  ax = fh.add_axes(

References

[1]

Anderson M. Winkler, Gerard R. Ridgway, Matthew A. Webster, Stephen M. Smith, and Thomas E. Nichols. Permutation inference for the general linear model. NeuroImage, 92:381–397, 2014. doi:10.1016/j.neuroimage.2014.01.060.

[2]

Marti J. Anderson and John Robinson. Permutation tests for linear models. Australian & New Zealand Journal of Statistics, 43(1):75–88, 2001. doi:10.1111/1467-842X.00156.

Estimated memory usage: 1013 MB