6.1. Extracting times series to build a functional connectome#

6.1.1. Time-series from a brain parcellation or “MaxProb” atlas#

6.1.1.1. Brain parcellations#

Regions used to extract the signal can be defined by a “hard” parcellation. For instance, the nilearn.datasets has functions to download atlases forming reference parcellation, e.g., fetch_atlas_craddock_2012, fetch_atlas_harvard_oxford, fetch_atlas_yeo_2011.

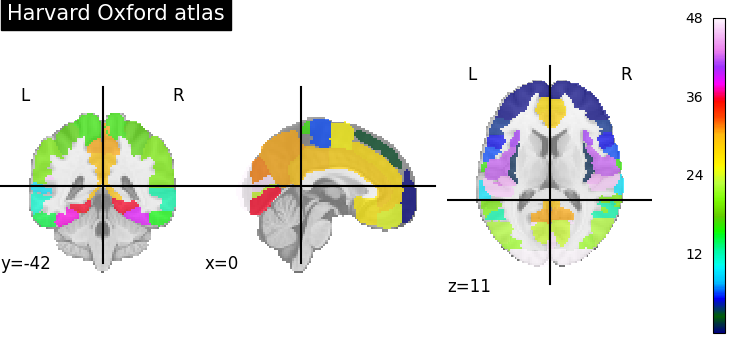
For instance to retrieve the Harvard-Oxford cortical parcellation, sampled at 2mm, and with a threshold of a probability of 0.25:

from nilearn import datasets
dataset = datasets.fetch_atlas_harvard_oxford('cort-maxprob-thr25-2mm')
atlas_filename = dataset.maps
labels = dataset.labels

Plotting can then be done as:

from nilearn import plotting
plotting.plot_roi(atlas_filename)
../_images/sphx_glr_plot_atlas_001.png

See also

6.1.1.2. Extracting signals on a parcellation#

To extract signal on the parcellation, the easiest option is to use the NiftiLabelsMasker. As any “maskers” in nilearn, it is a processing object that is created by specifying all the important parameters, but not the data:

from nilearn.maskers import NiftiLabelsMasker
masker = NiftiLabelsMasker(labels_img=atlas_filename, standardize=True)

The Nifti data can then be turned to time-series by calling the NiftiLabelsMasker.fit_transform method, that takes either filenames or NiftiImage objects:

time_series = masker.fit_transform(frmi_files,
                                   confounds=confounds_dataframe)

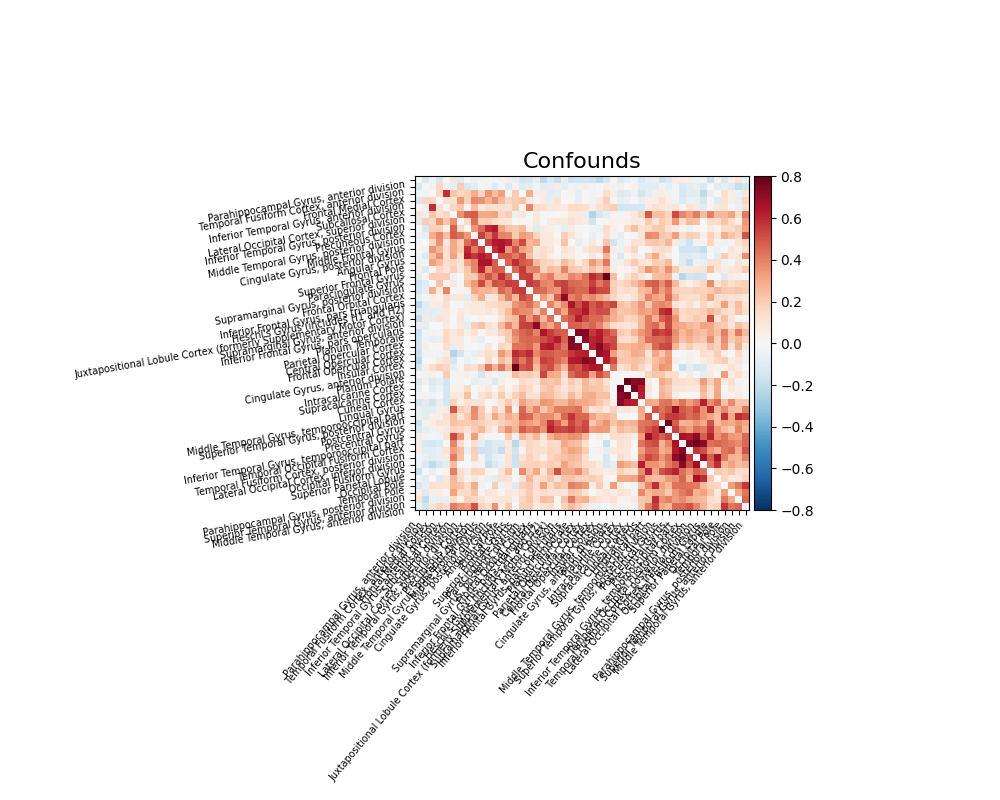
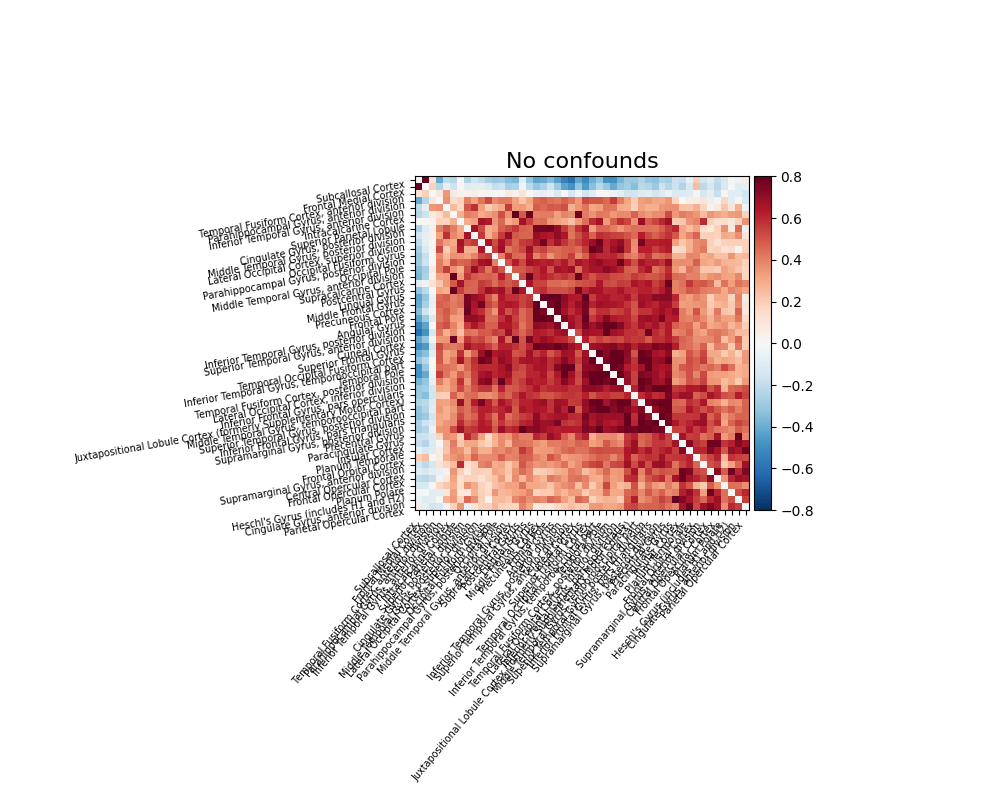
Note that confound signals can be specified in the call. Indeed, to obtain time series that capture well the functional interactions between regions, regressing out noise sources is very important (Varoquaux and Craddock[1]). For data processed by fMRIPrep, load_confounds and load_confounds_strategy can help you retrieve confound variables. load_confounds_strategy selects confounds based on past literature with limited parameters for customisation. For more freedoms of confounds selection, load_confounds groups confound variables as sets of noise components and one can fine tune each of the parameters.

../_images/sphx_glr_plot_signal_extraction_001.png ../_images/sphx_glr_plot_signal_extraction_002.png

6.1.2. Time-series from a probabilistic atlas#

6.1.2.1. Probabilistic atlases#

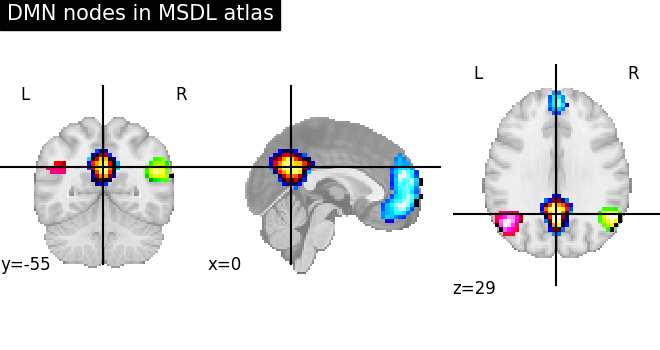
The definition of regions as by a continuous probability map captures better our imperfect knowledge of boundaries in brain images (notably because of inter-subject registration errors). One example of such an atlas well suited to resting-state or naturalistic-stimuli data analysis is the MSDL atlas (nilearn.datasets.fetch_atlas_msdl).

Probabilistic atlases are represented as a set of continuous maps, in a 4D nifti image. Visualization the atlas thus requires to visualize each of these maps, which requires accessing them with nilearn.image.index_img (see the corresponding example).

../_images/sphx_glr_plot_overlay_001.png

6.1.2.2. Extracting signals from a probabilistic atlas#

As with extraction of signals on a parcellation, extracting signals from a probabilistic atlas can be done with a “masker” object: the NiftiMapsMasker. It is created by specifying the important parameters, in particular the atlas:

from nilearn.maskers import NiftiMapsMasker
masker = NiftiMapsMasker(maps_img=atlas_filename, standardize=True)

The fit_transform method turns filenames or NiftiImage objects to time series:

time_series = masker.fit_transform(frmi_files, confounds=csv_file)

The procedure is the same as with brain parcellations but using the NiftiMapsMasker, and the same considerations on using confounds regressors apply.

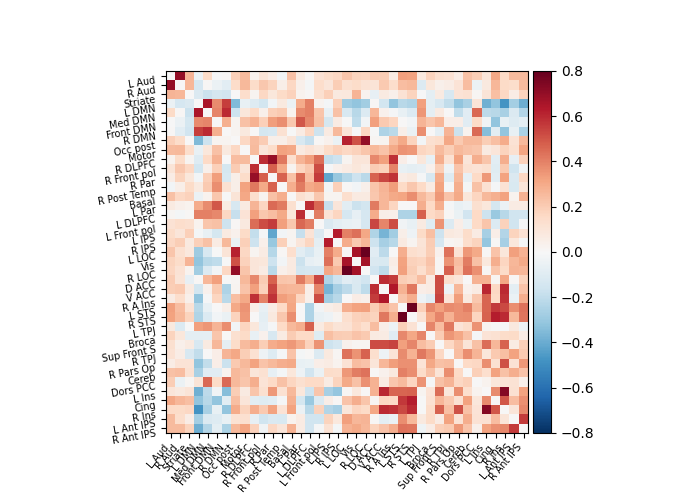
../_images/sphx_glr_plot_probabilistic_atlas_extraction_001.png

6.1.3. A functional connectome: a graph of interactions#

A square matrix, such as a correlation matrix, can also be seen as a “graph”: a set of “nodes”, connected by “edges”. When these nodes are brain regions, and the edges capture interactions between them, this graph is a “functional connectome”.

We can display it with the nilearn.plotting.plot_connectome function that take the matrix, and coordinates of the nodes in MNI space. In the case of the MSDL atlas (nilearn.datasets.fetch_atlas_msdl), the CSV file readily comes with MNI coordinates for each region (see for instance example: Extracting signals of a probabilistic atlas of functional regions).

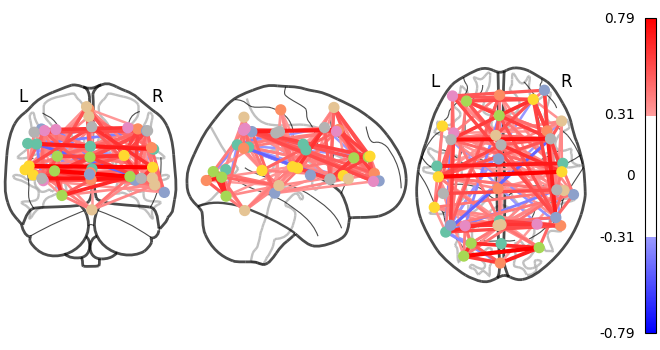
../_images/sphx_glr_plot_probabilistic_atlas_extraction_002.png

As you can see, the correlation matrix gives a very “full” graph: every node is connected to every other one. This is because it also captures indirect connections. In the next section we will see how to focus on direct connections only.

6.1.4. A functional connectome: extracting coordinates of regions#

For atlases without readily available label coordinates, center coordinates can be computed for each region on hard parcellation or probabilistic atlases.


6.1.4.1. References#