Single-subject data (two runs) in native space

The example shows the analysis of an SPM dataset, with two conditions: viewing a face image or a scrambled face image.

This example takes a lot of time because the input are lists of 3D images sampled in different positions (encoded by different affine functions).

See also

For more information see the dataset description.

Fetch and inspect the data

Fetch the SPM multimodal_faces data.

from nilearn.datasets import fetch_spm_multimodal_fmri

subject_data = fetch_spm_multimodal_fmri()

[fetch_spm_multimodal_fmri] Dataset created in
/home/runner/nilearn_data/spm_multimodal_fmri
[fetch_spm_multimodal_fmri] Missing 390 functional scans for session 1.
[fetch_spm_multimodal_fmri] Data absent, downloading...
[fetch_spm_multimodal_fmri] Downloading data from
https://www.fil.ion.ucl.ac.uk/spm/download/data/mmfaces/multimodal_fmri.zip ...
[fetch_spm_multimodal_fmri] Downloaded 1736704 of 134263085 bytes (1.3%%,
1.3min remaining)
[fetch_spm_multimodal_fmri] Downloaded 6324224 of 134263085 bytes (4.7%%,
41.6s remaining)
[fetch_spm_multimodal_fmri] Downloaded 10018816 of 134263085 bytes (7.5%%,
38.1s remaining)
[fetch_spm_multimodal_fmri] Downloaded 13770752 of 134263085 bytes (10.3%%,
35.6s remaining)
[fetch_spm_multimodal_fmri] Downloaded 17620992 of 134263085 bytes (13.1%%,
33.7s remaining)
[fetch_spm_multimodal_fmri] Downloaded 21708800 of 134263085 bytes (16.2%%,
31.6s remaining)
[fetch_spm_multimodal_fmri] Downloaded 25706496 of 134263085 bytes (19.1%%,
30.0s remaining)
[fetch_spm_multimodal_fmri] Downloaded 29556736 of 134263085 bytes (22.0%%,
28.7s remaining)
[fetch_spm_multimodal_fmri] Downloaded 33677312 of 134263085 bytes (25.1%%,
27.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 37437440 of 134263085 bytes (27.9%%,
26.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 41697280 of 134263085 bytes (31.1%%,
24.7s remaining)
[fetch_spm_multimodal_fmri] Downloaded 46096384 of 134263085 bytes (34.3%%,
23.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 50348032 of 134263085 bytes (37.5%%,
21.9s remaining)
[fetch_spm_multimodal_fmri] Downloaded 55418880 of 134263085 bytes (41.3%%,
20.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 60997632 of 134263085 bytes (45.4%%,
18.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 66723840 of 134263085 bytes (49.7%%,
16.4s remaining)
[fetch_spm_multimodal_fmri] Downloaded 73474048 of 134263085 bytes (54.7%%,
14.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 79126528 of 134263085 bytes (58.9%%,
12.7s remaining)
[fetch_spm_multimodal_fmri] Downloaded 84852736 of 134263085 bytes (63.2%%,
11.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 90079232 of 134263085 bytes (67.1%%,
9.9s remaining)
[fetch_spm_multimodal_fmri] Downloaded 95150080 of 134263085 bytes (70.9%%,
8.7s remaining)
[fetch_spm_multimodal_fmri] Downloaded 99147776 of 134263085 bytes (73.8%%,
7.9s remaining)
[fetch_spm_multimodal_fmri] Downloaded 103186432 of 134263085 bytes (76.9%%,
7.0s remaining)
[fetch_spm_multimodal_fmri] Downloaded 107479040 of 134263085 bytes (80.1%%,
6.0s remaining)
[fetch_spm_multimodal_fmri] Downloaded 111525888 of 134263085 bytes (83.1%%,
5.1s remaining)
[fetch_spm_multimodal_fmri] Downloaded 115965952 of 134263085 bytes (86.4%%,
4.1s remaining)
[fetch_spm_multimodal_fmri] Downloaded 120471552 of 134263085 bytes (89.7%%,
3.1s remaining)
[fetch_spm_multimodal_fmri] Downloaded 124592128 of 134263085 bytes (92.8%%,
2.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 129048576 of 134263085 bytes (96.1%%,
1.2s remaining)
[fetch_spm_multimodal_fmri] Downloaded 132816896 of 134263085 bytes (98.9%%,
0.3s remaining)
[fetch_spm_multimodal_fmri]  ...done. (32 seconds, 0 min)

[fetch_spm_multimodal_fmri] Extracting data from
/home/runner/nilearn_data/spm_multimodal_fmri/sub001/multimodal_fmri.zip...
[fetch_spm_multimodal_fmri] .. done.

[fetch_spm_multimodal_fmri] Downloading data from
https://www.fil.ion.ucl.ac.uk/spm/download/data/mmfaces/multimodal_smri.zip ...
[fetch_spm_multimodal_fmri] Downloaded 1687552 of 6852766 bytes (24.6%%,    3.3s
remaining)
[fetch_spm_multimodal_fmri]  ...done. (3 seconds, 0 min)

[fetch_spm_multimodal_fmri] Extracting data from
/home/runner/nilearn_data/spm_multimodal_fmri/sub001/multimodal_smri.zip...
[fetch_spm_multimodal_fmri] .. done.

Let’s inspect one of the event files before using them.

import pandas as pd

events = [subject_data.events1, subject_data.events2]

events_dataframe = pd.read_csv(events[0], sep="\t")
events_dataframe["trial_type"].value_counts()

trial_type
scrambled    86
faces        64
Name: count, dtype: int64

We can confirm there are only 2 conditions in the dataset.

from nilearn.plotting import plot_event, show

plot_event(events)

show()

/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:41: UserWarning:

You are using the 'agg' matplotlib backend that is non-interactive.
No figure will be plotted when calling matplotlib.pyplot.show() or nilearn.plotting.show().
You can fix this by installing a different backend: for example via
        pip install PyQt6

Resample the images: this is achieved by the concat_imgs function of Nilearn.

import warnings

from nilearn.image import concat_imgs, mean_img, resample_img

# Avoid getting too many warnings due to resampling
with warnings.catch_warnings():
    warnings.simplefilter("ignore")
    fmri_img = [
        concat_imgs(subject_data.func1, auto_resample=True),
        concat_imgs(subject_data.func2, auto_resample=True),
    ]
affine, shape = fmri_img[0].affine, fmri_img[0].shape
print("Resampling the second image (this takes time)...")
fmri_img[1] = resample_img(fmri_img[1], affine, shape[:3])

Resampling the second image (this takes time)...

Let’s create mean image for display purposes.

mean_image = mean_img(fmri_img)

Fit the model

Fit the GLM for the 2 runs by specifying a FirstLevelModel and then fitting it.

# Sample at the beginning of each acquisition.
slice_time_ref = 0.0
# We use a discrete cosine transform to model signal drifts.
drift_model = "cosine"
# The cutoff for the drift model is 0.01 Hz.
high_pass = 0.01
# The hemodynamic response function
hrf_model = "spm + derivative"

from nilearn.glm.first_level import FirstLevelModel

print("Fitting a GLM")
fmri_glm = FirstLevelModel(
    smoothing_fwhm=None,
    t_r=subject_data.t_r,
    hrf_model=hrf_model,
    drift_model=drift_model,
    high_pass=high_pass,
    verbose=1,
)


fmri_glm = fmri_glm.fit(fmri_img, events=events)

Fitting a GLM
[FirstLevelModel.fit] Loading data from <nibabel.nifti1.Nifti1Image object at
0x7f1ecfde8040>
[FirstLevelModel.fit] Computing mask
[FirstLevelModel.fit] Resampling mask
[FirstLevelModel.fit] Finished fit
[FirstLevelModel.fit] Computing run 1 out of 2 runs (go take a coffee, a big
one).
[FirstLevelModel.fit] Performing mask computation.
[FirstLevelModel.fit] Loading data from <nibabel.nifti1.Nifti1Image object at
0x7f1ecfde8040>
[FirstLevelModel.fit] Extracting region signals
[FirstLevelModel.fit] Cleaning extracted signals
[FirstLevelModel.fit] Masking took 1 seconds.
[FirstLevelModel.fit] Performing GLM computation.
[FirstLevelModel.fit] GLM took 1 seconds.
[FirstLevelModel.fit] Computing run 2 out of 2 runs (2 seconds remaining).
[FirstLevelModel.fit] Performing mask computation.
[FirstLevelModel.fit] Loading data from <nibabel.nifti1.Nifti1Image object at
0x7f1f0cf8d510>
[FirstLevelModel.fit] Extracting region signals
[FirstLevelModel.fit] Cleaning extracted signals
[FirstLevelModel.fit] Masking took 1 seconds.
[FirstLevelModel.fit] Performing GLM computation.
[FirstLevelModel.fit] GLM took 1 seconds.
[FirstLevelModel.fit] Computation of 2 runs done in 5 seconds.

View the results

Now we can compute contrast-related statistical maps (in z-scale), and plot them.

from nilearn.plotting import plot_stat_map

print("Computing contrasts")

Computing contrasts

We actually want more interesting contrasts. The simplest contrast just makes the difference between the two main conditions. We define the two opposite versions to run one-tailed t-tests.

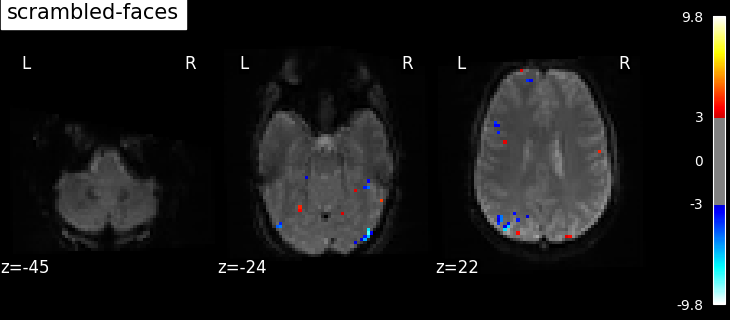
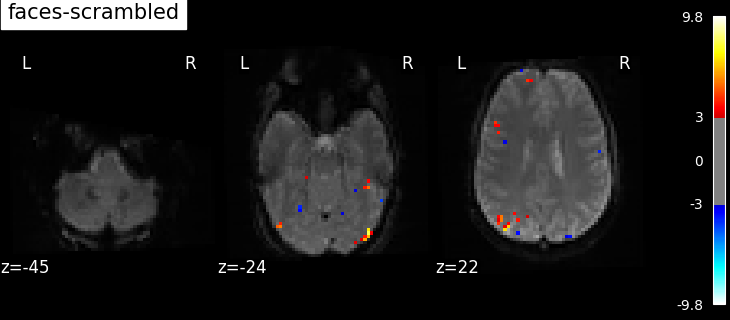
contrasts = ["faces - scrambled", "scrambled - faces"]

Let’s store common parameters for all plots.

We plot the contrasts values overlaid on the mean fMRI image and we will use the z-score values as transparency, with any voxel with | Z-score | > 3 being fully opaque and any voxel with 0 < | Z-score | < 1.96 being partly transparent.

plot_param = {
    "vmin": 0,
    "display_mode": "z",
    "cut_coords": 3,
    "black_bg": True,
    "bg_img": mean_image,
    "cmap": "inferno",
    "transparency_range": [0, 3],
}

# Iterate on contrasts to compute and plot them.
for contrast_id in contrasts:
    print(f"\tcontrast id: {contrast_id}")

    results = fmri_glm.compute_contrast(contrast_id, output_type="all")

    plot_stat_map(
        results["stat"],
        title=contrast_id,
        transparency=results["z_score"],
        **plot_param,
    )

• 
• 

        contrast id: faces - scrambled
/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:134: RuntimeWarning:

The same contrast will be used for all 2 runs. If the design matrices are not the same for all runs, (for example with different column names or column order across runs) you should pass contrast as an expression using the name of the conditions as they appear in the design matrices.

[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
        contrast id: scrambled - faces
/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:134: RuntimeWarning:

The same contrast will be used for all 2 runs. If the design matrices are not the same for all runs, (for example with different column names or column order across runs) you should pass contrast as an expression using the name of the conditions as they appear in the design matrices.

[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals

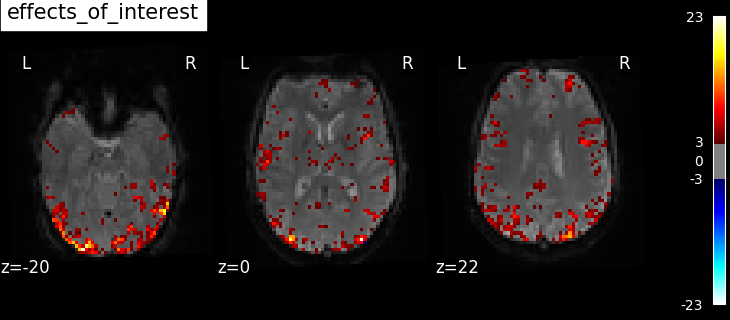
We also define the effects of interest contrast, a 2-dimensional contrasts spanning the two conditions.

import numpy as np

contrasts = np.eye(2)

results = fmri_glm.compute_contrast(contrasts, output_type="all")

plot_stat_map(
    results["stat"],
    title="effects of interest",
    transparency=results["z_score"],
    **plot_param,
)

show()

/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:151: RuntimeWarning:

The same contrast will be used for all 2 runs. If the design matrices are not the same for all runs, (for example with different column names or column order across runs) you should pass contrast as an expression using the name of the conditions as they appear in the design matrices.

/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:151: UserWarning:

F contrasts should have 20 columns, but it has only 2. The rest of the contrast was padded with zeros.

/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:151: UserWarning:

Running approximate fixed effects on F statistics.

[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
[FirstLevelModel.compute_contrast] Computing image from signals
/home/runner/work/nilearn/nilearn/examples/04_glm_first_level/plot_spm_multimodal_faces.py:160: UserWarning:

You are using the 'agg' matplotlib backend that is non-interactive.
No figure will be plotted when calling matplotlib.pyplot.show() or nilearn.plotting.show().
You can fix this by installing a different backend: for example via
        pip install PyQt6

Based on the resulting maps we observe that the analysis results in wide activity for the ‘effects of interest’ contrast, showing the implications of large portions of the visual cortex in the conditions. By contrast, the differential effect between “faces” and “scrambled” involves sparser, more anterior and lateral regions. It also displays some responses in the frontal lobe.

Estimated memory usage: 1034 MB