Note
Click here to download the full example code or to run this example in your browser via Binder
9.5.10. Predicted time series and residuals¶
Here we fit a First Level GLM with the minimize_memory-argument set to False. By doing so, the FirstLevelModel-object stores the residuals, which we can then inspect. Also, the predicted time series can be extracted, which is useful to assess the quality of the model fit.
Note
If you are using Nilearn with a version older than 0.9.0, then you should either upgrade your version or import maskers from the input_data module instead of the maskers module.
That is, you should manually replace in the following example all occurrences of:
from nilearn.maskers import NiftiMasker
with:
from nilearn.input_data import NiftiMasker
9.5.10.1. Import modules¶
from nilearn.datasets import fetch_spm_auditory
from nilearn import image
from nilearn import masking
import pandas as pd
# load fMRI data
subject_data = fetch_spm_auditory()
fmri_img = image.concat_imgs(subject_data.func)
# Make an average
mean_img = image.mean_img(fmri_img)
mask = masking.compute_epi_mask(mean_img)
# Clean and smooth data
fmri_img = image.clean_img(fmri_img, standardize=False)
fmri_img = image.smooth_img(fmri_img, 5.)
# load events
events = pd.read_table(subject_data['events'])
9.5.10.2. Fit model¶
Note that minimize_memory is set to False so that FirstLevelModel stores the residuals. signal_scaling is set to False, so we keep the same scaling as the original data in fmri_img.
from nilearn.glm.first_level import FirstLevelModel
fmri_glm = FirstLevelModel(t_r=7,
drift_model='cosine',
signal_scaling=False,
mask_img=mask,
minimize_memory=False)
fmri_glm = fmri_glm.fit(fmri_img, events)
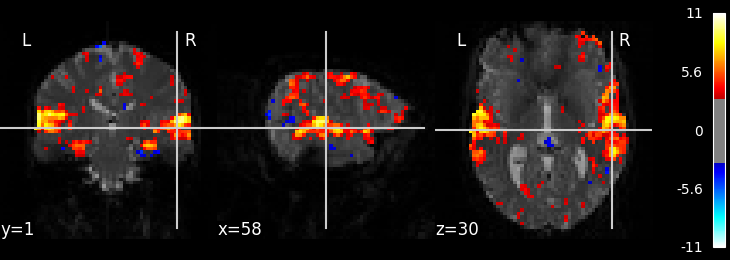
9.5.10.3. Calculate and plot contrast¶
from nilearn import plotting
z_map = fmri_glm.compute_contrast('active - rest')
plotting.plot_stat_map(z_map, bg_img=mean_img, threshold=3.1)
Out:
<nilearn.plotting.displays._slicers.OrthoSlicer object at 0x7fa5013f14f0>
9.5.10.4. Extract the largest clusters¶
from nilearn.reporting import get_clusters_table
from nilearn.maskers import NiftiSpheresMasker
table = get_clusters_table(z_map, stat_threshold=3.1,
cluster_threshold=20).set_index('Cluster ID', drop=True)
table.head()
# get the 6 largest clusters' max x, y, and z coordinates
coords = table.loc[range(1, 7), ['X', 'Y', 'Z']].values
# extract time series from each coordinate
masker = NiftiSpheresMasker(coords)
real_timeseries = masker.fit_transform(fmri_img)
predicted_timeseries = masker.fit_transform(fmri_glm.predicted[0])
9.5.10.5. Plot predicted and actual time series for 6 most significant clusters¶
import matplotlib.pyplot as plt
# colors for each of the clusters
colors = ['blue', 'navy', 'purple', 'magenta', 'olive', 'teal']
# plot the time series and corresponding locations
fig1, axs1 = plt.subplots(2, 6)
for i in range(0, 6):
# plotting time series
axs1[0, i].set_title('Cluster peak {}\n'.format(coords[i]))
axs1[0, i].plot(real_timeseries[:, i], c=colors[i], lw=2)
axs1[0, i].plot(predicted_timeseries[:, i], c='r', ls='--', lw=2)
axs1[0, i].set_xlabel('Time')
axs1[0, i].set_ylabel('Signal intensity', labelpad=0)
# plotting image below the time series
roi_img = plotting.plot_stat_map(
z_map, cut_coords=[coords[i][2]], threshold=3.1, figure=fig1,
axes=axs1[1, i], display_mode='z', colorbar=False, bg_img=mean_img)
roi_img.add_markers([coords[i]], colors[i], 300)
fig1.set_size_inches(24, 14)
![Cluster peak [-60. -6. 42.] , Cluster peak [60. 0. 36.] , Cluster peak [30. -9. 12.] , Cluster peak [-27. -3. 15.] , Cluster peak [57. 21. 75.] , Cluster peak [39. 33. 51.]](../../_images/sphx_glr_plot_predictions_residuals_002.png)
9.5.10.6. Get residuals¶
Out:
/home/nicolas/GitRepos/nilearn-fork/nilearn/glm/regression.py:42: FutureWarning:
'resid' has been deprecated in version 0.7.0 and will be removed in version 0.9.0. Please use 'residuals' instead.
9.5.10.7. Plot distribution of residuals¶
Note that residuals are not really distributed normally.
![Cluster peak [-60. -6. 42.] , Cluster peak [60. 0. 36.] , Cluster peak [30. -9. 12.] , Cluster peak [-27. -3. 15.] , Cluster peak [57. 21. 75.] , Cluster peak [39. 33. 51.]](../../_images/sphx_glr_plot_predictions_residuals_003.png)
Out:
Mean residuals: 4.440892098500626e-15
Mean residuals: -0.05424369099334821
Mean residuals: 0.0023122829555654403
Mean residuals: 0.011694403952940005
Mean residuals: 0.002376300178617674
Mean residuals: -0.004645997877150698
9.5.10.8. Plot R-squared¶
Because we stored the residuals, we can plot the R-squared: the proportion of explained variance of the GLM as a whole. Note that the R-squared is markedly lower deep down the brain, where there is more physiological noise and we are further away from the receive coils. However, R-Squared should be interpreted with a grain of salt. The R-squared value will necessarily increase with the addition of more factors (such as rest, active, drift, motion) into the GLM. Additionally, we are looking at the overall fit of the model, so we are unable to say whether a voxel/region has a large R-squared value because the voxel/region is responsive to the experiment (such as active or rest) or because the voxel/region fits the noise factors (such as drift or motion) that could be present in the GLM. To isolate the influence of the experiment, we can use an F-test as shown in the next section.
plotting.plot_stat_map(fmri_glm.r_square[0], bg_img=mean_img, threshold=.1,
display_mode='z', cut_coords=7)

Out:
<nilearn.plotting.displays._slicers.ZSlicer object at 0x7fa5006b4ac0>
9.5.10.9. Calculate and Plot F-test¶
The F-test tells you how well the GLM fits effects of interest such as the active and rest conditions together. This is different from R-squared, which tells you how well the overall GLM fits the data, including active, rest and all the other columns in the design matrix such as drift and motion.
import numpy as np
design_matrix = fmri_glm.design_matrices_[0]
# contrast with a one for "active" and zero everywhere else
active = np.array([1 if c == 'active' else 0 for c in design_matrix.columns])
# contrast with a one for "rest" and zero everywhere else
rest = np.array([1 if c == 'rest' else 0 for c in design_matrix.columns])
effects_of_interest = np.vstack((active, rest))
# f-test for rest and activity
z_map_ftest = fmri_glm.compute_contrast(
effects_of_interest,
stat_type='F',
output_type='z_score')
plotting.plot_stat_map(z_map_ftest, bg_img=mean_img, threshold=3.1,
display_mode='z', cut_coords=7)

Out:
<nilearn.plotting.displays._slicers.ZSlicer object at 0x7fa541511f40>
Total running time of the script: ( 0 minutes 35.968 seconds)
Estimated memory usage: 539 MB
