Note

This page is a reference documentation. It only explains the class signature, and not how to use it. Please refer to the user guide for the big picture.

8.12.4. nilearn.glm.ARModel

class nilearn.glm.ARModel(design, rho)

A regression model with an AR(p) covariance structure.

In terms of a LikelihoodModel, the parameters are beta, the usual regression parameters, and sigma, a scalar nuisance parameter that shows up as multiplier in front of the AR(p) covariance.

__init__(design, rho)

Initialize AR model instance

Parameters:

design : ndarray

2D array with design matrix

rho : int or array-like

If int, gives order of model, and initializes rho to zeros. If ndarray, gives initial estimate of rho. Be careful as ARModel(X, 1) != ARModel(X, 1.0).

df_resid()
fit(Y)

Fit model to data Y

Full fit of the model including estimate of covariance matrix, (whitened) residuals and scale.

Parameters:

Y : array-like

The dependent variable for the Least Squares problem.

Returns:

fit : RegressionResults

initialize(design)
logL(beta, Y, nuisance=None)

Returns the value of the loglikelihood function at beta.

Given the whitened design matrix, the loglikelihood is evaluated at the parameter vector, beta, for the dependent variable, Y and the nuisance parameter, sigma.

Parameters:

beta : ndarray

The parameter estimates. Must be of length df_model.

Y : ndarray

The dependent variable

nuisance : dict, optional

A dict with key ‘sigma’, which is an optional estimate of sigma. If None, defaults to its maximum likelihood estimate (with beta fixed) as sum((Y - X*beta)**2) / n, where n=Y.shape[0], X=self.design.

Returns:

loglf : float

The value of the loglikelihood function.

Notes

The log-Likelihood Function is defined as

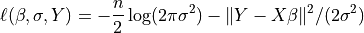
\ell(\beta,\sigma,Y)= -\frac{n}{2}\log(2\pi\sigma^2) - \|Y-X\beta\|^2/(2\sigma^2)

The parameter 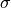\sigma above is what is sometimes referred to as a nuisance parameter. That is, the likelihood is considered as a function of 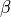\beta, but to evaluate it, a value of 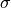\sigma is needed.

If 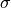\sigma is not provided, then its maximum likelihood estimate: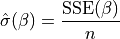

\hat{\sigma}(\beta) = \frac{\text{SSE}(\beta)}{n}

is plugged in. This likelihood is now a function of only 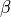\beta and is technically referred to as a profile-likelihood.

References

    1. Green. “Econometric Analysis,” 5th ed., Pearson, 2003.
wdesign()
whiten(X)

Whiten a series of columns according to AR(p) covariance structure

Parameters:

X : array-like of shape (n_features)

array to whiten

Returns:

whitened_X : ndarray

X whitened with order self.order AR