Note
Go to the end to download the full example code or to run this example in your browser via Binder
Voxel-Based Morphometry on Oasis dataset#
This example uses Voxel-Based Morphometry (VBM) to study the relationship between aging and gray matter density.
The data come from the OASIS project. If you use it, you need to agree with the data usage agreement available on the website.
It has been run through a standard VBM pipeline (using SPM8 and NewSegment) to create VBM maps, which we study here.
Predictive modeling analysis: VBM bio-markers of aging?#
We run a standard SVM-ANOVA nilearn pipeline to predict age from the VBM data. We use only 100 subjects from the OASIS dataset to limit the memory usage.
Note that for an actual predictive modeling study of aging, the study should be ran on the full set of subjects. Also, all parameters should be set by cross-validation. This includes the smoothing applied to the data and the number of features selected by the ANOVA step. Indeed, even these data-preparation parameter impact significantly the prediction score.
Also, parameters such as the smoothing should be applied to the data and the number of features selected by the ANOVA step should be set by nested cross-validation, as they impact significantly the prediction score.
Brain mapping with mass univariate#
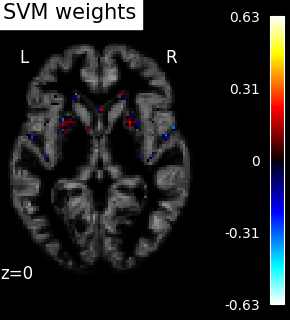
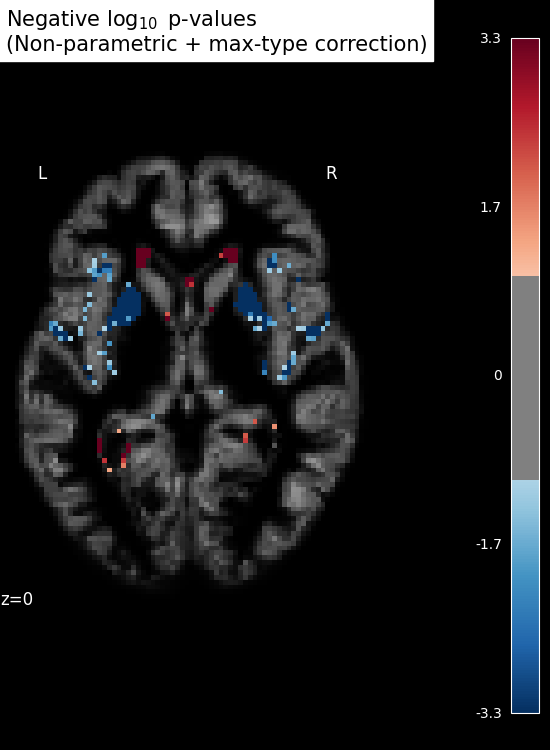
SVM weights are very noisy, partly because heavy smoothing is detrimental for the prediction here. A standard analysis using mass-univariate GLM (here permuted to have exact correction for multiple comparisons) gives a much clearer view of the important regions.
Note
If you are using Nilearn with a version older than 0.9.0, then you should either upgrade your version or import maskers from the input_data module instead of the maskers module.
That is, you should manually replace in the following example all occurrences of:
from nilearn.maskers import NiftiMasker
with:
from nilearn.input_data import NiftiMasker
import matplotlib.pyplot as plt
import numpy as np
from nilearn import datasets
from nilearn.image import get_data
from nilearn.maskers import NiftiMasker
n_subjects = 100 # more subjects requires more memory
Load Oasis dataset#
oasis_dataset = datasets.fetch_oasis_vbm(
n_subjects=n_subjects, legacy_format=False
)
gray_matter_map_filenames = oasis_dataset.gray_matter_maps
age = oasis_dataset.ext_vars["age"].values
# Split data into training set and test set
from sklearn.model_selection import train_test_split
gm_imgs_train, gm_imgs_test, age_train, age_test = train_test_split(
gray_matter_map_filenames, age, train_size=0.6, random_state=0
)
# print basic information on the dataset
print(
"First gray-matter anatomy image (3D) is located at: "
f"{oasis_dataset.gray_matter_maps[0]}"
)
print(
"First white-matter anatomy image (3D) is located at: "
f"{oasis_dataset.white_matter_maps[0]}"
)
First gray-matter anatomy image (3D) is located at: /home/remi/nilearn_data/oasis1/OAS1_0001_MR1/mwrc1OAS1_0001_MR1_mpr_anon_fslswapdim_bet.nii.gz
First white-matter anatomy image (3D) is located at: /home/remi/nilearn_data/oasis1/OAS1_0001_MR1/mwrc2OAS1_0001_MR1_mpr_anon_fslswapdim_bet.nii.gz
Preprocess data#
nifti_masker = NiftiMasker(
standardize=False, smoothing_fwhm=2, memory="nilearn_cache"
) # cache options
gm_maps_masked = nifti_masker.fit_transform(gm_imgs_train)
# The features with too low between-subject variance are removed using
# :class:`sklearn.feature_selection.VarianceThreshold`.
from sklearn.feature_selection import VarianceThreshold
variance_threshold = VarianceThreshold(threshold=0.01)
variance_threshold.fit_transform(gm_maps_masked)
# Then we convert the data back to the mask image in order to use it for
# decoding process
mask = nifti_masker.inverse_transform(variance_threshold.get_support())
Prediction pipeline with ANOVA and SVR using nilearn.decoding.DecoderRegressor Object
# In nilearn we can benefit from the built-in DecoderRegressor object to
# do ANOVA with SVR instead of manually defining the whole pipeline.
# This estimator also uses Cross Validation to select best models and ensemble
# them. Furthermore, you can pass n_jobs=<some_high_value> to the
# DecoderRegressor class to take advantage of a multi-core system.
# To save time (because these are anat images with many voxels), we include
# only the 1-percent voxels most correlated with the age variable to fit. We
# also want to set mask hyperparameter to be the mask we just obtained above.
from nilearn.decoding import DecoderRegressor
decoder = DecoderRegressor(
estimator="svr",
mask=mask,
scoring="neg_mean_absolute_error",
screening_percentile=1,
n_jobs=1,
standardize="zscore_sample",
)
# Fit and predict with the decoder
decoder.fit(gm_imgs_train, age_train)
# Sort test data for better visualization (trend, etc.)
perm = np.argsort(age_test)[::-1]
age_test = age_test[perm]
gm_imgs_test = np.array(gm_imgs_test)[perm]
age_pred = decoder.predict(gm_imgs_test)
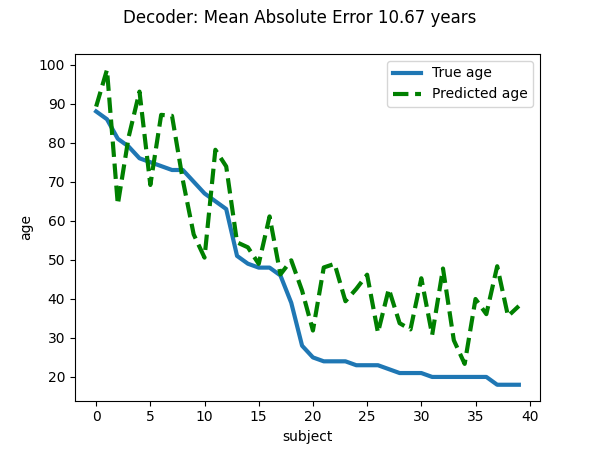
prediction_score = -np.mean(decoder.cv_scores_["beta"])
print("=== DECODER ===")
print(f"explained variance for the cross-validation: {prediction_score:f}")
print()
=== DECODER ===
explained variance for the cross-validation: 10.670599
Visualization#
weight_img = decoder.coef_img_["beta"]
# Create the figure
from nilearn.plotting import plot_stat_map, show
bg_filename = gray_matter_map_filenames[0]
z_slice = 0
display = plot_stat_map(
weight_img, bg_img=bg_filename, display_mode="z", cut_coords=[z_slice]
)
display.title("SVM weights")
show()
Visualize the quality of predictions#
plt.figure(figsize=(6, 4.5))
plt.suptitle(f"Decoder: Mean Absolute Error {prediction_score:.2f} years")
linewidth = 3
plt.plot(age_test, label="True age", linewidth=linewidth)
plt.plot(age_pred, "--", c="g", label="Predicted age", linewidth=linewidth)
plt.ylabel("age")
plt.xlabel("subject")
plt.legend(loc="best")
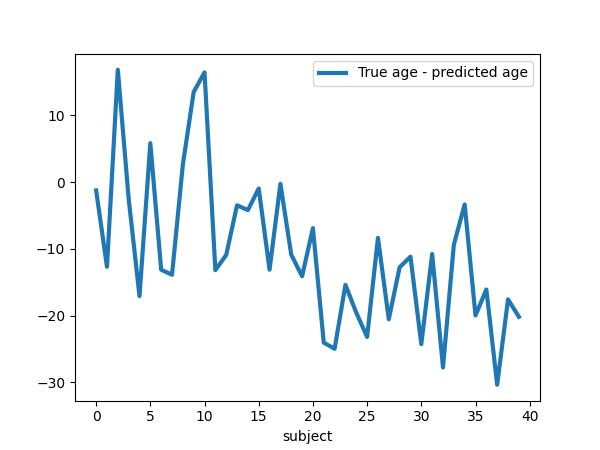
plt.figure(figsize=(6, 4.5))
plt.plot(
age_test - age_pred, label="True age - predicted age", linewidth=linewidth
)
plt.xlabel("subject")
plt.legend(loc="best")
<matplotlib.legend.Legend object at 0x7fd1f23ec590>
Inference with massively univariate model#
print("Massively univariate model")
gm_maps_masked = NiftiMasker().fit_transform(gray_matter_map_filenames)
data = variance_threshold.fit_transform(gm_maps_masked)
# Statistical inference
from nilearn.mass_univariate import permuted_ols
# This can be changed to use more CPUs.
neg_log_pvals, t_scores_original_data, _ = permuted_ols(
age,
data, # + intercept as a covariate by default
n_perm=2000, # 1,000 in the interest of time; 10000 would be better
verbose=1, # display progress bar
n_jobs=1,
)
signed_neg_log_pvals = neg_log_pvals * np.sign(t_scores_original_data)
signed_neg_log_pvals_unmasked = nifti_masker.inverse_transform(
variance_threshold.inverse_transform(signed_neg_log_pvals)
)
# Show results
threshold = -np.log10(0.1) # 10% corrected
fig = plt.figure(figsize=(5.5, 7.5), facecolor="k")
display = plot_stat_map(
signed_neg_log_pvals_unmasked,
bg_img=bg_filename,
threshold=threshold,
cmap=plt.cm.RdBu_r,
display_mode="z",
cut_coords=[z_slice],
figure=fig,
)
title = (
"Negative $\\log_{10}$ p-values" "\n(Non-parametric + max-type correction)"
)
display.title(title)
n_detections = (get_data(signed_neg_log_pvals_unmasked) > threshold).sum()
print(f"\n{int(n_detections)} detections")
show()
Massively univariate model
Job #1, processed 0/2000 permutations (0.00%, 222.47552871704102 seconds remaining)
Job #1, processed 10/2000 permutations (0.50%, 58.82723426818848 seconds remaining)
Job #1, processed 20/2000 permutations (1.00%, 49.08793115615845 seconds remaining)
Job #1, processed 30/2000 permutations (1.50%, 46.42307798067729 seconds remaining)
Job #1, processed 40/2000 permutations (2.00%, 45.57533049583435 seconds remaining)
Job #1, processed 50/2000 permutations (2.50%, 47.26395106315613 seconds remaining)
Job #1, processed 60/2000 permutations (3.00%, 49.239974180857345 seconds remaining)
Job #1, processed 70/2000 permutations (3.50%, 50.93145905222212 seconds remaining)
Job #1, processed 80/2000 permutations (4.00%, 49.52055358886719 seconds remaining)
Job #1, processed 90/2000 permutations (4.50%, 48.488787439134384 seconds remaining)
Job #1, processed 100/2000 permutations (5.00%, 47.501522064208984 seconds remaining)
Job #1, processed 110/2000 permutations (5.50%, 48.315023465590045 seconds remaining)
Job #1, processed 120/2000 permutations (6.00%, 47.62662124633789 seconds remaining)
Job #1, processed 130/2000 permutations (6.50%, 48.82316875457764 seconds remaining)
Job #1, processed 140/2000 permutations (7.00%, 49.38646858079093 seconds remaining)
Job #1, processed 150/2000 permutations (7.50%, 49.485080560048424 seconds remaining)
Job #1, processed 160/2000 permutations (8.00%, 48.63966464996338 seconds remaining)
Job #1, processed 170/2000 permutations (8.50%, 47.68716784084545 seconds remaining)
Job #1, processed 180/2000 permutations (9.00%, 47.26353780428568 seconds remaining)
Job #1, processed 190/2000 permutations (9.50%, 47.46540970551341 seconds remaining)
Job #1, processed 200/2000 permutations (10.00%, 46.91712713241577 seconds remaining)
Job #1, processed 210/2000 permutations (10.50%, 46.40350529125759 seconds remaining)
Job #1, processed 220/2000 permutations (11.00%, 45.905873927203096 seconds remaining)
Job #1, processed 230/2000 permutations (11.50%, 45.35661475554757 seconds remaining)
Job #1, processed 240/2000 permutations (12.00%, 44.87558968861897 seconds remaining)
Job #1, processed 250/2000 permutations (12.50%, 44.726048707962036 seconds remaining)
Job #1, processed 260/2000 permutations (13.00%, 44.30427602621225 seconds remaining)
Job #1, processed 270/2000 permutations (13.50%, 44.028435936680545 seconds remaining)
Job #1, processed 280/2000 permutations (14.00%, 43.717721939086914 seconds remaining)
Job #1, processed 290/2000 permutations (14.50%, 43.43798942401491 seconds remaining)
Job #1, processed 300/2000 permutations (15.00%, 43.19881661732992 seconds remaining)
Job #1, processed 310/2000 permutations (15.50%, 42.73886401422562 seconds remaining)
Job #1, processed 320/2000 permutations (16.00%, 42.290353775024414 seconds remaining)
Job #1, processed 330/2000 permutations (16.50%, 42.34405930114515 seconds remaining)
Job #1, processed 340/2000 permutations (17.00%, 42.13338990772472 seconds remaining)
Job #1, processed 350/2000 permutations (17.50%, 41.629641090120586 seconds remaining)
Job #1, processed 360/2000 permutations (18.00%, 41.21443120638529 seconds remaining)
Job #1, processed 370/2000 permutations (18.50%, 41.17431671554978 seconds remaining)
Job #1, processed 380/2000 permutations (19.00%, 40.77507064217016 seconds remaining)
Job #1, processed 390/2000 permutations (19.50%, 40.31381817353078 seconds remaining)
Job #1, processed 400/2000 permutations (20.00%, 39.894636154174805 seconds remaining)
Job #1, processed 410/2000 permutations (20.50%, 39.61044844185434 seconds remaining)
Job #1, processed 420/2000 permutations (21.00%, 39.19186277616592 seconds remaining)
Job #1, processed 430/2000 permutations (21.50%, 38.81711612191311 seconds remaining)
Job #1, processed 440/2000 permutations (22.00%, 38.43071599440141 seconds remaining)
Job #1, processed 450/2000 permutations (22.50%, 38.169065184063385 seconds remaining)
Job #1, processed 460/2000 permutations (23.00%, 38.10783467085465 seconds remaining)
Job #1, processed 470/2000 permutations (23.50%, 37.89416057505506 seconds remaining)
Job #1, processed 480/2000 permutations (24.00%, 37.52923520406087 seconds remaining)
Job #1, processed 490/2000 permutations (24.50%, 37.18472890951195 seconds remaining)
Job #1, processed 500/2000 permutations (25.00%, 37.08070921897888 seconds remaining)
Job #1, processed 510/2000 permutations (25.50%, 36.76232425839293 seconds remaining)
Job #1, processed 520/2000 permutations (26.00%, 36.42762593122629 seconds remaining)
Job #1, processed 530/2000 permutations (26.50%, 36.29309591707194 seconds remaining)
Job #1, processed 540/2000 permutations (27.00%, 36.17676902700354 seconds remaining)
Job #1, processed 550/2000 permutations (27.50%, 35.80693130059676 seconds remaining)
Job #1, processed 560/2000 permutations (28.00%, 35.477959973471506 seconds remaining)
Job #1, processed 570/2000 permutations (28.50%, 35.16201495287711 seconds remaining)
Job #1, processed 580/2000 permutations (29.00%, 34.875569129812305 seconds remaining)
Job #1, processed 590/2000 permutations (29.50%, 34.60451561717664 seconds remaining)
Job #1, processed 600/2000 permutations (30.00%, 34.30487394332886 seconds remaining)
Job #1, processed 610/2000 permutations (30.50%, 34.117158878045004 seconds remaining)
Job #1, processed 620/2000 permutations (31.00%, 33.942975259596295 seconds remaining)
Job #1, processed 630/2000 permutations (31.50%, 33.63791586860778 seconds remaining)
Job #1, processed 640/2000 permutations (32.00%, 33.33260229229927 seconds remaining)
Job #1, processed 650/2000 permutations (32.50%, 33.021045409716095 seconds remaining)
Job #1, processed 660/2000 permutations (33.00%, 32.82380658207518 seconds remaining)
Job #1, processed 670/2000 permutations (33.50%, 32.839505056836714 seconds remaining)
Job #1, processed 680/2000 permutations (34.00%, 32.568795709049 seconds remaining)
Job #1, processed 690/2000 permutations (34.50%, 32.27129797659058 seconds remaining)
Job #1, processed 700/2000 permutations (35.00%, 31.98634151050023 seconds remaining)
Job #1, processed 710/2000 permutations (35.50%, 31.749444854091593 seconds remaining)
Job #1, processed 720/2000 permutations (36.00%, 31.448559231228298 seconds remaining)
Job #1, processed 730/2000 permutations (36.50%, 31.141046697146272 seconds remaining)
Job #1, processed 740/2000 permutations (37.00%, 30.88237616822526 seconds remaining)
Job #1, processed 750/2000 permutations (37.50%, 30.622330109278362 seconds remaining)
Job #1, processed 760/2000 permutations (38.00%, 30.382966706627293 seconds remaining)
Job #1, processed 770/2000 permutations (38.50%, 30.14768842907695 seconds remaining)
Job #1, processed 780/2000 permutations (39.00%, 29.938228429892124 seconds remaining)
Job #1, processed 790/2000 permutations (39.50%, 29.685675892648817 seconds remaining)
Job #1, processed 800/2000 permutations (40.00%, 29.42202115058899 seconds remaining)
Job #1, processed 810/2000 permutations (40.50%, 29.156523713359128 seconds remaining)
Job #1, processed 820/2000 permutations (41.00%, 28.912662942235063 seconds remaining)
Job #1, processed 830/2000 permutations (41.50%, 28.750437653208355 seconds remaining)
Job #1, processed 840/2000 permutations (42.00%, 28.64367195538112 seconds remaining)
Job #1, processed 850/2000 permutations (42.50%, 28.43370050542495 seconds remaining)
Job #1, processed 860/2000 permutations (43.00%, 28.20147314737009 seconds remaining)
Job #1, processed 870/2000 permutations (43.50%, 27.976664724021123 seconds remaining)
Job #1, processed 880/2000 permutations (44.00%, 27.800689393823795 seconds remaining)
Job #1, processed 890/2000 permutations (44.50%, 27.614770760696924 seconds remaining)
Job #1, processed 900/2000 permutations (45.00%, 27.380835559633045 seconds remaining)
Job #1, processed 910/2000 permutations (45.50%, 27.19955801963806 seconds remaining)
Job #1, processed 920/2000 permutations (46.00%, 26.981257656346198 seconds remaining)
Job #1, processed 930/2000 permutations (46.50%, 26.719771636429655 seconds remaining)
Job #1, processed 940/2000 permutations (47.00%, 26.470411970260294 seconds remaining)
Job #1, processed 950/2000 permutations (47.50%, 26.244568686736258 seconds remaining)
Job #1, processed 960/2000 permutations (48.00%, 26.008816878000893 seconds remaining)
Job #1, processed 970/2000 permutations (48.50%, 25.772832292871378 seconds remaining)
Job #1, processed 980/2000 permutations (49.00%, 25.534941994414037 seconds remaining)
Job #1, processed 990/2000 permutations (49.50%, 25.275560118935324 seconds remaining)
Job #1, processed 1000/2000 permutations (50.00%, 25.03720235824585 seconds remaining)
Job #1, processed 1010/2000 permutations (50.50%, 24.852299175640145 seconds remaining)
Job #1, processed 1020/2000 permutations (51.00%, 24.614781809788123 seconds remaining)
Job #1, processed 1030/2000 permutations (51.50%, 24.333482094181395 seconds remaining)
Job #1, processed 1040/2000 permutations (52.00%, 24.10169946230375 seconds remaining)
Job #1, processed 1050/2000 permutations (52.50%, 23.90081852958316 seconds remaining)
Job #1, processed 1060/2000 permutations (53.00%, 23.669113694496875 seconds remaining)
Job #1, processed 1070/2000 permutations (53.50%, 23.453102154152415 seconds remaining)
Job #1, processed 1080/2000 permutations (54.00%, 23.202997384247958 seconds remaining)
Job #1, processed 1090/2000 permutations (54.50%, 22.987424898585047 seconds remaining)
Job #1, processed 1100/2000 permutations (55.00%, 22.706706242127854 seconds remaining)
Job #1, processed 1110/2000 permutations (55.50%, 22.466782967249554 seconds remaining)
Job #1, processed 1120/2000 permutations (56.00%, 22.22477012021201 seconds remaining)
Job #1, processed 1130/2000 permutations (56.50%, 21.987447434822013 seconds remaining)
Job #1, processed 1140/2000 permutations (57.00%, 21.73218367392557 seconds remaining)
Job #1, processed 1150/2000 permutations (57.50%, 21.47715035728786 seconds remaining)
Job #1, processed 1160/2000 permutations (58.00%, 21.22246687987755 seconds remaining)
Job #1, processed 1170/2000 permutations (58.50%, 20.977281651945198 seconds remaining)
Job #1, processed 1180/2000 permutations (59.00%, 20.79321376347946 seconds remaining)
Job #1, processed 1190/2000 permutations (59.50%, 20.587281445495222 seconds remaining)
Job #1, processed 1200/2000 permutations (60.00%, 20.363059361775715 seconds remaining)
Job #1, processed 1210/2000 permutations (60.50%, 20.09590788715142 seconds remaining)
Job #1, processed 1220/2000 permutations (61.00%, 19.848372553215654 seconds remaining)
Job #1, processed 1230/2000 permutations (61.50%, 19.611074455385285 seconds remaining)
Job #1, processed 1240/2000 permutations (62.00%, 19.35900564347544 seconds remaining)
Job #1, processed 1250/2000 permutations (62.50%, 19.101172971725465 seconds remaining)
Job #1, processed 1260/2000 permutations (63.00%, 18.83039284887768 seconds remaining)
Job #1, processed 1270/2000 permutations (63.50%, 18.588445849306 seconds remaining)
Job #1, processed 1280/2000 permutations (64.00%, 18.36214891076088 seconds remaining)
Job #1, processed 1290/2000 permutations (64.50%, 18.09680513633314 seconds remaining)
Job #1, processed 1300/2000 permutations (65.00%, 17.853067031273476 seconds remaining)
Job #1, processed 1310/2000 permutations (65.50%, 17.596222498944698 seconds remaining)
Job #1, processed 1320/2000 permutations (66.00%, 17.39253911105069 seconds remaining)
Job #1, processed 1330/2000 permutations (66.50%, 17.13880380652005 seconds remaining)
Job #1, processed 1340/2000 permutations (67.00%, 16.88910481111327 seconds remaining)
Job #1, processed 1350/2000 permutations (67.50%, 16.712102280722725 seconds remaining)
Job #1, processed 1360/2000 permutations (68.00%, 16.46072073543773 seconds remaining)
Job #1, processed 1370/2000 permutations (68.50%, 16.228189940000103 seconds remaining)
Job #1, processed 1380/2000 permutations (69.00%, 15.98424710398135 seconds remaining)
Job #1, processed 1390/2000 permutations (69.50%, 15.732615225606684 seconds remaining)
Job #1, processed 1400/2000 permutations (70.00%, 15.481214250837052 seconds remaining)
Job #1, processed 1410/2000 permutations (70.50%, 15.237010769810237 seconds remaining)
Job #1, processed 1420/2000 permutations (71.00%, 14.993096318043454 seconds remaining)
Job #1, processed 1430/2000 permutations (71.50%, 14.76049906223804 seconds remaining)
Job #1, processed 1440/2000 permutations (72.00%, 14.532062782181635 seconds remaining)
Job #1, processed 1450/2000 permutations (72.50%, 14.313832447446625 seconds remaining)
Job #1, processed 1460/2000 permutations (73.00%, 14.07124570624469 seconds remaining)
Job #1, processed 1470/2000 permutations (73.50%, 13.826089333514778 seconds remaining)
Job #1, processed 1480/2000 permutations (74.00%, 13.603852884189504 seconds remaining)
Job #1, processed 1490/2000 permutations (74.50%, 13.34370119779702 seconds remaining)
Job #1, processed 1500/2000 permutations (75.00%, 13.09323755900065 seconds remaining)
Job #1, processed 1510/2000 permutations (75.50%, 12.83035245478548 seconds remaining)
Job #1, processed 1520/2000 permutations (76.00%, 12.58322178690057 seconds remaining)
Job #1, processed 1530/2000 permutations (76.50%, 12.327862359339896 seconds remaining)
Job #1, processed 1540/2000 permutations (77.00%, 12.065250666110547 seconds remaining)
Job #1, processed 1550/2000 permutations (77.50%, 11.804288979499571 seconds remaining)
Job #1, processed 1560/2000 permutations (78.00%, 11.54022913101392 seconds remaining)
Job #1, processed 1570/2000 permutations (78.50%, 11.290385474065307 seconds remaining)
Job #1, processed 1580/2000 permutations (79.00%, 11.032663849335682 seconds remaining)
Job #1, processed 1590/2000 permutations (79.50%, 10.776618456690565 seconds remaining)
Job #1, processed 1600/2000 permutations (80.00%, 10.513851702213287 seconds remaining)
Job #1, processed 1610/2000 permutations (80.50%, 10.244842569280115 seconds remaining)
Job #1, processed 1620/2000 permutations (81.00%, 9.988933990031112 seconds remaining)
Job #1, processed 1630/2000 permutations (81.50%, 9.71748790711713 seconds remaining)
Job #1, processed 1640/2000 permutations (82.00%, 9.460117648287516 seconds remaining)
Job #1, processed 1650/2000 permutations (82.50%, 9.201263565005679 seconds remaining)
Job #1, processed 1660/2000 permutations (83.00%, 8.938064618283008 seconds remaining)
Job #1, processed 1670/2000 permutations (83.50%, 8.67335877875368 seconds remaining)
Job #1, processed 1680/2000 permutations (84.00%, 8.40919744400751 seconds remaining)
Job #1, processed 1690/2000 permutations (84.50%, 8.161847877784593 seconds remaining)
Job #1, processed 1700/2000 permutations (85.00%, 7.899367795271033 seconds remaining)
Job #1, processed 1710/2000 permutations (85.50%, 7.642558721073886 seconds remaining)
Job #1, processed 1720/2000 permutations (86.00%, 7.383287291194118 seconds remaining)
Job #1, processed 1730/2000 permutations (86.50%, 7.121414852969219 seconds remaining)
Job #1, processed 1740/2000 permutations (87.00%, 6.857476903104234 seconds remaining)
Job #1, processed 1750/2000 permutations (87.50%, 6.598994459424699 seconds remaining)
Job #1, processed 1760/2000 permutations (88.00%, 6.33606108752164 seconds remaining)
Job #1, processed 1770/2000 permutations (88.50%, 6.07301024797946 seconds remaining)
Job #1, processed 1780/2000 permutations (89.00%, 5.816065552529325 seconds remaining)
Job #1, processed 1790/2000 permutations (89.50%, 5.558963118984712 seconds remaining)
Job #1, processed 1800/2000 permutations (90.00%, 5.3029722107781305 seconds remaining)
Job #1, processed 1810/2000 permutations (90.50%, 5.039848267044151 seconds remaining)
Job #1, processed 1820/2000 permutations (91.00%, 4.775380336321317 seconds remaining)
Job #1, processed 1830/2000 permutations (91.50%, 4.512631629985538 seconds remaining)
Job #1, processed 1840/2000 permutations (92.00%, 4.247497620789901 seconds remaining)
Job #1, processed 1850/2000 permutations (92.50%, 3.9807005379651046 seconds remaining)
Job #1, processed 1860/2000 permutations (93.00%, 3.721448103586833 seconds remaining)
Job #1, processed 1870/2000 permutations (93.50%, 3.45413659473154 seconds remaining)
Job #1, processed 1880/2000 permutations (94.00%, 3.187204675471529 seconds remaining)
Job #1, processed 1890/2000 permutations (94.50%, 2.9219843584393694 seconds remaining)
Job #1, processed 1900/2000 permutations (95.00%, 2.659018918087608 seconds remaining)
Job #1, processed 1910/2000 permutations (95.50%, 2.393983103217879 seconds remaining)
Job #1, processed 1920/2000 permutations (96.00%, 2.1309022804101305 seconds remaining)
Job #1, processed 1930/2000 permutations (96.50%, 1.8656492171509895 seconds remaining)
Job #1, processed 1940/2000 permutations (97.00%, 1.599018522144593 seconds remaining)
Job #1, processed 1950/2000 permutations (97.50%, 1.3320516500717554 seconds remaining)
Job #1, processed 1960/2000 permutations (98.00%, 1.0653705256325856 seconds remaining)
Job #1, processed 1970/2000 permutations (98.50%, 0.7998007481473351 seconds remaining)
Job #1, processed 1980/2000 permutations (99.00%, 0.5330767679696131 seconds remaining)
Job #1, processed 1990/2000 permutations (99.50%, 0.26655306768177744 seconds remaining)
1970 detections
Total running time of the script: (1 minutes 33.896 seconds)
Estimated memory usage: 1922 MB