Note
Click here to download the full example code or to run this example in your browser via Binder
Example of MRI response functions#
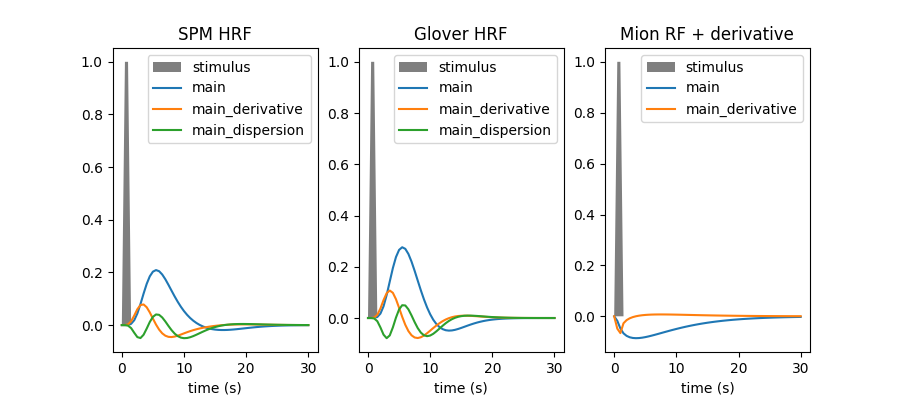
Within this example we are going to plot the hemodynamic response function (HRF) model in SPM together with the HRF shape proposed by G.Glover, as well as their time and dispersion derivatives. We also illustrate how users can input a custom response function, which can for instance be useful when dealing with non human primate data acquired using a contrast agent. In our case, we input a custom response function for MION, a common agent used to enhance contrast on MRI images of monkeys.
The HRF is the filter which couples neural responses to the metabolic-related changes in the MRI signal. HRF models are simply phenomenological.
In current analysis frameworks, the choice of HRF model is essentially left to the user. Fortunately, using the SPM or Glover model does not make a huge difference. Adding derivatives should be considered whenever timing information has some degree of uncertainty, and is actually useful to detect timing issues.
This example requires matplotlib and scipy.
Define stimulus parameters and response models#
To get an impulse response, we simulate a single event occurring at time t=0, with duration 1s.
import numpy as np
time_length = 30.0
frame_times = np.linspace(0, time_length, 61)
onset, amplitude, duration = 0.0, 1.0, 1.0
exp_condition = np.array((onset, duration, amplitude)).reshape(3, 1)
Make a time array of this condition for display:
stim = np.zeros_like(frame_times)
stim[(frame_times > onset) * (frame_times <= onset + duration)] = amplitude
Define custom response functions for MION. Custom response functions should at least take tr and oversampling as arguments:
from scipy.stats import gamma
def mion_response_function(tr, oversampling=16, onset=0.0):
"""Implementation of the MION response function model.
Parameters
----------
tr: float
scan repeat time, in seconds
oversampling: int, optional
temporal oversampling factor
onset: float, optional
hrf onset time, in seconds
Returns
-------
response_function: array of shape(length / tr * oversampling, dtype=float)
response_function sampling on the oversampled time grid
"""
dt = tr / oversampling
time_stamps = np.linspace(
0, time_length, np.rint(time_length / dt).astype(int)
)
time_stamps -= onset
# parameters of the gamma function
delay = 1.55
dispersion = 5.5
response_function = gamma.pdf(time_stamps, delay, loc=0, scale=dispersion)
response_function /= response_function.sum()
response_function *= -1
return response_function
def mion_time_derivative(tr, oversampling=16.0):
"""Implementation of the MION time derivative response function model.
Parameters
----------
tr: float
scan repeat time, in seconds
oversampling: int, optional
temporal oversampling factor, optional
Returns
-------
drf: array of shape(time_length / tr * oversampling, dtype=float)
derived_response_function sampling on the provided grid
"""
do = 0.1
drf = (
mion_response_function(tr, oversampling)
- mion_response_function(tr, oversampling, do)
) / do
return drf
Define response function models to be displayed:
rf_models = [
("spm + derivative + dispersion", "SPM HRF", None),
("glover + derivative + dispersion", "Glover HRF", None),
(
[mion_response_function, mion_time_derivative],
"Mion RF + derivative",
["main", "main_derivative"],
),
]
Sample and plot response functions#
import matplotlib.pyplot as plt
from nilearn.glm.first_level import compute_regressor
oversampling = 16
fig = plt.figure(figsize=(9, 4))
for i, (rf_model, model_title, labels) in enumerate(rf_models):
# compute signal of interest by convolution
signal, _labels = compute_regressor(
exp_condition,
rf_model,
frame_times,
con_id="main",
oversampling=oversampling,
)
# plot signal
plt.subplot(1, len(rf_models), i + 1)
plt.fill(frame_times, stim, "k", alpha=0.5, label="stimulus")
for j in range(signal.shape[1]):
plt.plot(
frame_times,
signal.T[j],
label=(
labels[j]
if labels is not None
else (_labels[j] if _labels is not None else None)
),
)
plt.xlabel("time (s)")
plt.legend(loc=1)
plt.title(model_title)
# adjust plot
plt.subplots_adjust(bottom=0.12)
plt.show()
Total running time of the script: ( 0 minutes 3.011 seconds)
Estimated memory usage: 9 MB