Note
Click here to download the full example code or to run this example in your browser via Binder
Voxel-Based Morphometry on Oasis dataset#
This example uses Voxel-Based Morphometry (VBM) to study the relationship between aging and gray matter density.
The data come from the OASIS project. If you use it, you need to agree with the data usage agreement available on the website.
It has been run through a standard VBM pipeline (using SPM8 and NewSegment) to create VBM maps, which we study here.
Predictive modeling analysis: VBM bio-markers of aging?#
We run a standard SVM-ANOVA nilearn pipeline to predict age from the VBM data. We use only 100 subjects from the OASIS dataset to limit the memory usage.
Note that for an actual predictive modeling study of aging, the study should be ran on the full set of subjects. Also, all parameters should be set by cross-validation. This includes the smoothing applied to the data and the number of features selected by the ANOVA step. Indeed, even these data-preparation parameter impact significantly the prediction score.
Also, parameters such as the smoothing should be applied to the data and the number of features selected by the ANOVA step should be set by nested cross-validation, as they impact significantly the prediction score.
Brain mapping with mass univariate#
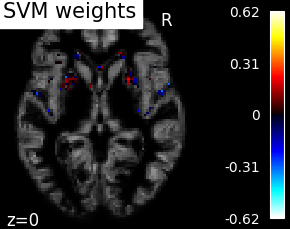
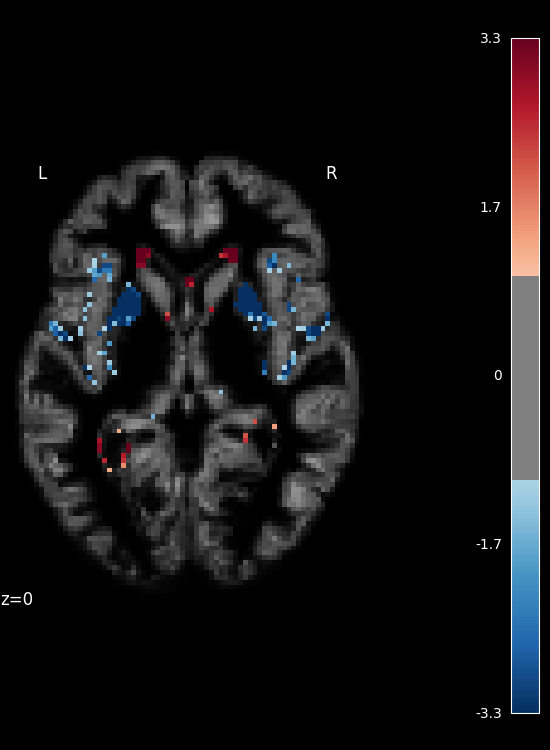
SVM weights are very noisy, partly because heavy smoothing is detrimental for the prediction here. A standard analysis using mass-univariate GLM (here permuted to have exact correction for multiple comparisons) gives a much clearer view of the important regions.
Note
If you are using Nilearn with a version older than 0.9.0, then you should either upgrade your version or import maskers from the input_data module instead of the maskers module.
That is, you should manually replace in the following example all occurrences of:
from nilearn.maskers import NiftiMasker
with:
from nilearn.input_data import NiftiMasker
# Authors: Elvis Dhomatob, <elvis.dohmatob@inria.fr>, Apr. 2014
# Virgile Fritsch, <virgile.fritsch@inria.fr>, Apr 2014
# Gael Varoquaux, Apr 2014
# Andres Hoyos-Idrobo, Apr 2017
import numpy as np
import matplotlib.pyplot as plt
from nilearn import datasets
from nilearn.maskers import NiftiMasker
from nilearn.image import get_data
n_subjects = 100 # more subjects requires more memory
Load Oasis dataset#
oasis_dataset = datasets.fetch_oasis_vbm(
n_subjects=n_subjects, legacy_format=False
)
gray_matter_map_filenames = oasis_dataset.gray_matter_maps
age = oasis_dataset.ext_vars['age'].values
# Split data into training set and test set
from sklearn.model_selection import train_test_split
gm_imgs_train, gm_imgs_test, age_train, age_test = train_test_split(
gray_matter_map_filenames, age, train_size=.6, random_state=0)
# print basic information on the dataset
print('First gray-matter anatomy image (3D) is located at: %s' %
oasis_dataset.gray_matter_maps[0]) # 3D data
print('First white-matter anatomy image (3D) is located at: %s' %
oasis_dataset.white_matter_maps[0]) # 3D data
First gray-matter anatomy image (3D) is located at: /home/yasmin/nilearn/nilearn_data/oasis1/OAS1_0001_MR1/mwrc1OAS1_0001_MR1_mpr_anon_fslswapdim_bet.nii.gz
First white-matter anatomy image (3D) is located at: /home/yasmin/nilearn/nilearn_data/oasis1/OAS1_0001_MR1/mwrc2OAS1_0001_MR1_mpr_anon_fslswapdim_bet.nii.gz
Preprocess data#
nifti_masker = NiftiMasker(
standardize=False,
smoothing_fwhm=2,
memory='nilearn_cache') # cache options
gm_maps_masked = nifti_masker.fit_transform(gm_imgs_train)
# The features with too low between-subject variance are removed using
# :class:`sklearn.feature_selection.VarianceThreshold`.
from sklearn.feature_selection import VarianceThreshold
variance_threshold = VarianceThreshold(threshold=.01)
gm_maps_thresholded = variance_threshold.fit_transform(gm_maps_masked)
# Then we convert the data back to the mask image in order to use it for
# decoding process
mask = nifti_masker.inverse_transform(variance_threshold.get_support())
Prediction pipeline with ANOVA and SVR using nilearn.decoding.DecoderRegressor Object
# In nilearn we can benefit from the built-in DecoderRegressor object to
# do ANOVA with SVR instead of manually defining the whole pipeline.
# This estimator also uses Cross Validation to select best models and ensemble
# them. Furthermore, you can pass n_jobs=<some_high_value> to the
# DecoderRegressor class to take advantage of a multi-core system.
# To save time (because these are anat images with many voxels), we include
# only the 1-percent voxels most correlated with the age variable to fit. We
# also want to set mask hyperparameter to be the mask we just obtained above.
from nilearn.decoding import DecoderRegressor
decoder = DecoderRegressor(estimator='svr', mask=mask,
scoring='neg_mean_absolute_error',
screening_percentile=1,
n_jobs=1)
# Fit and predict with the decoder
decoder.fit(gm_imgs_train, age_train)
# Sort test data for better visualization (trend, etc.)
perm = np.argsort(age_test)[::-1]
age_test = age_test[perm]
gm_imgs_test = np.array(gm_imgs_test)[perm]
age_pred = decoder.predict(gm_imgs_test)
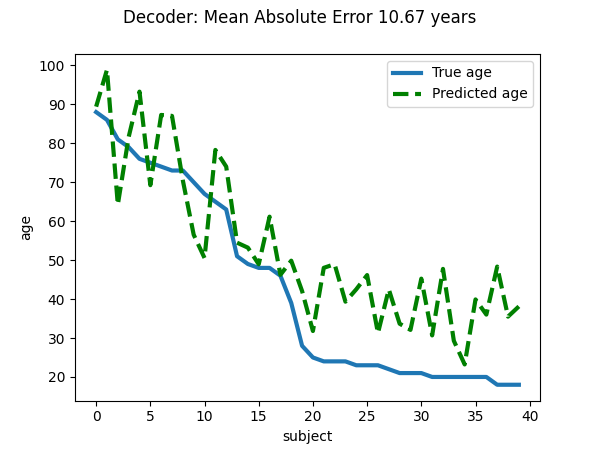
prediction_score = -np.mean(decoder.cv_scores_['beta'])
print("=== DECODER ===")
print("explained variance for the cross-validation: %f" % prediction_score)
print()
=== DECODER ===
explained variance for the cross-validation: 10.670598
Visualization#
weight_img = decoder.coef_img_['beta']
# Create the figure
from nilearn.plotting import plot_stat_map, show
bg_filename = gray_matter_map_filenames[0]
z_slice = 0
display = plot_stat_map(weight_img, bg_img=bg_filename,
display_mode='z', cut_coords=[z_slice])
display.title("SVM weights")
show()
Visualize the quality of predictions#
plt.figure(figsize=(6, 4.5))
plt.suptitle("Decoder: Mean Absolute Error %.2f years" % prediction_score)
linewidth = 3
plt.plot(age_test, label="True age", linewidth=linewidth)
plt.plot(age_pred, '--', c="g", label="Predicted age", linewidth=linewidth)
plt.ylabel("age")
plt.xlabel("subject")
plt.legend(loc="best")
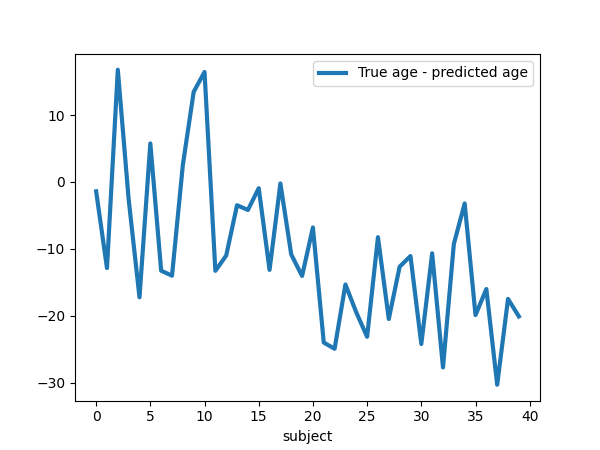
plt.figure(figsize=(6, 4.5))
plt.plot(age_test - age_pred, label="True age - predicted age",
linewidth=linewidth)
plt.xlabel("subject")
plt.legend(loc="best")
<matplotlib.legend.Legend object at 0x7fc1a9443790>
Inference with massively univariate model#
print("Massively univariate model")
gm_maps_masked = NiftiMasker().fit_transform(gray_matter_map_filenames)
data = variance_threshold.fit_transform(gm_maps_masked)
# Statistical inference
from nilearn.mass_univariate import permuted_ols
neg_log_pvals, t_scores_original_data, _ = permuted_ols(
age, data, # + intercept as a covariate by default
n_perm=2000, # 1,000 in the interest of time; 10000 would be better
verbose=1, # display progress bar
n_jobs=1) # can be changed to use more CPUs
signed_neg_log_pvals = neg_log_pvals * np.sign(t_scores_original_data)
signed_neg_log_pvals_unmasked = nifti_masker.inverse_transform(
variance_threshold.inverse_transform(signed_neg_log_pvals))
# Show results
threshold = -np.log10(0.1) # 10% corrected
fig = plt.figure(figsize=(5.5, 7.5), facecolor='k')
display = plot_stat_map(signed_neg_log_pvals_unmasked, bg_img=bg_filename,
threshold=threshold, cmap=plt.cm.RdBu_r,
display_mode='z', cut_coords=[z_slice],
figure=fig)
title = ('Negative $\\log_{10}$ p-values'
'\n(Non-parametric + max-type correction)')
display.title(title, y=1.2)
n_detections = (get_data(signed_neg_log_pvals_unmasked) > threshold).sum()
print('\n%d detections' % n_detections)
show()
Massively univariate model
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
Job #1, processed 0/2000 permutations (0.00%, 258.944034576416 seconds remaining)
Job #1, processed 10/2000 permutations (0.50%, 52.62660837173462 seconds remaining)
Job #1, processed 20/2000 permutations (1.00%, 48.62601184844971 seconds remaining)
Job #1, processed 30/2000 permutations (1.50%, 46.57935770352682 seconds remaining)
Job #1, processed 40/2000 permutations (2.00%, 47.70808959007263 seconds remaining)
Job #1, processed 50/2000 permutations (2.50%, 47.29413342475891 seconds remaining)
Job #1, processed 60/2000 permutations (3.00%, 47.10188897450765 seconds remaining)
Job #1, processed 70/2000 permutations (3.50%, 46.95309955733163 seconds remaining)
Job #1, processed 80/2000 permutations (4.00%, 46.89876365661621 seconds remaining)
Job #1, processed 90/2000 permutations (4.50%, 46.26135940021938 seconds remaining)
Job #1, processed 100/2000 permutations (5.00%, 45.7080864906311 seconds remaining)
Job #1, processed 110/2000 permutations (5.50%, 45.36008373173801 seconds remaining)
Job #1, processed 120/2000 permutations (6.00%, 45.003063122431435 seconds remaining)
Job #1, processed 130/2000 permutations (6.50%, 44.74668108499967 seconds remaining)
Job #1, processed 140/2000 permutations (7.00%, 44.50059740883964 seconds remaining)
Job #1, processed 150/2000 permutations (7.50%, 44.17677696545919 seconds remaining)
Job #1, processed 160/2000 permutations (8.00%, 43.80268585681915 seconds remaining)
Job #1, processed 170/2000 permutations (8.50%, 43.65399111018462 seconds remaining)
Job #1, processed 180/2000 permutations (9.00%, 43.383035288916695 seconds remaining)
Job #1, processed 190/2000 permutations (9.50%, 43.06463212715953 seconds remaining)
Job #1, processed 200/2000 permutations (10.00%, 42.67679500579834 seconds remaining)
Job #1, processed 210/2000 permutations (10.50%, 42.42097384589059 seconds remaining)
Job #1, processed 220/2000 permutations (11.00%, 42.05239961364053 seconds remaining)
Job #1, processed 230/2000 permutations (11.50%, 41.800495862960815 seconds remaining)
Job #1, processed 240/2000 permutations (12.00%, 41.59397029876709 seconds remaining)
Job #1, processed 250/2000 permutations (12.50%, 41.39133286476135 seconds remaining)
Job #1, processed 260/2000 permutations (13.00%, 41.14573574066162 seconds remaining)
Job #1, processed 270/2000 permutations (13.50%, 40.82333902076439 seconds remaining)
Job #1, processed 280/2000 permutations (14.00%, 40.57219484874181 seconds remaining)
Job #1, processed 290/2000 permutations (14.50%, 40.303012798572404 seconds remaining)
Job #1, processed 300/2000 permutations (15.00%, 40.10344934463501 seconds remaining)
Job #1, processed 310/2000 permutations (15.50%, 39.8265515681236 seconds remaining)
Job #1, processed 320/2000 permutations (16.00%, 39.56562477350235 seconds remaining)
Job #1, processed 330/2000 permutations (16.50%, 39.32997857440601 seconds remaining)
Job #1, processed 340/2000 permutations (17.00%, 39.12709585358115 seconds remaining)
Job #1, processed 350/2000 permutations (17.50%, 38.9010329246521 seconds remaining)
Job #1, processed 360/2000 permutations (18.00%, 38.69002283944024 seconds remaining)
Job #1, processed 370/2000 permutations (18.50%, 38.54092074084926 seconds remaining)
Job #1, processed 380/2000 permutations (19.00%, 38.27058084387529 seconds remaining)
Job #1, processed 390/2000 permutations (19.50%, 37.94659896997305 seconds remaining)
Job #1, processed 400/2000 permutations (20.00%, 37.806867599487305 seconds remaining)
Job #1, processed 410/2000 permutations (20.50%, 37.56025120688648 seconds remaining)
Job #1, processed 420/2000 permutations (21.00%, 37.27328958965483 seconds remaining)
Job #1, processed 430/2000 permutations (21.50%, 37.018978268601174 seconds remaining)
Job #1, processed 440/2000 permutations (22.00%, 36.702895402908325 seconds remaining)
Job #1, processed 450/2000 permutations (22.50%, 36.56745465596517 seconds remaining)
Job #1, processed 460/2000 permutations (23.00%, 36.27016062321871 seconds remaining)
Job #1, processed 470/2000 permutations (23.50%, 36.01854111793193 seconds remaining)
Job #1, processed 480/2000 permutations (24.00%, 35.737126906712845 seconds remaining)
Job #1, processed 490/2000 permutations (24.50%, 35.47589275301719 seconds remaining)
Job #1, processed 500/2000 permutations (25.00%, 35.28843355178833 seconds remaining)
Job #1, processed 510/2000 permutations (25.50%, 35.050522668688906 seconds remaining)
Job #1, processed 520/2000 permutations (26.00%, 34.75290657923772 seconds remaining)
Job #1, processed 530/2000 permutations (26.50%, 34.514929006684504 seconds remaining)
Job #1, processed 540/2000 permutations (27.00%, 34.26128480169508 seconds remaining)
Job #1, processed 550/2000 permutations (27.50%, 34.058713934638284 seconds remaining)
Job #1, processed 560/2000 permutations (28.00%, 33.81262881415231 seconds remaining)
Job #1, processed 570/2000 permutations (28.50%, 33.60706173327931 seconds remaining)
Job #1, processed 580/2000 permutations (29.00%, 33.37663419493313 seconds remaining)
Job #1, processed 590/2000 permutations (29.50%, 33.1770839731572 seconds remaining)
Job #1, processed 600/2000 permutations (30.00%, 32.95440856615703 seconds remaining)
Job #1, processed 610/2000 permutations (30.50%, 32.679548627040425 seconds remaining)
Job #1, processed 620/2000 permutations (31.00%, 32.443176477186135 seconds remaining)
Job #1, processed 630/2000 permutations (31.50%, 32.19070258216252 seconds remaining)
Job #1, processed 640/2000 permutations (32.00%, 31.975932717323303 seconds remaining)
Job #1, processed 650/2000 permutations (32.50%, 31.724569394038276 seconds remaining)
Job #1, processed 660/2000 permutations (33.00%, 31.446048122463804 seconds remaining)
Job #1, processed 670/2000 permutations (33.50%, 31.24844722961312 seconds remaining)
Job #1, processed 680/2000 permutations (34.00%, 30.982465940363266 seconds remaining)
Job #1, processed 690/2000 permutations (34.50%, 30.73050216315449 seconds remaining)
Job #1, processed 700/2000 permutations (35.00%, 30.460579872131348 seconds remaining)
Job #1, processed 710/2000 permutations (35.50%, 30.190506119123647 seconds remaining)
Job #1, processed 720/2000 permutations (36.00%, 29.959332784016926 seconds remaining)
Job #1, processed 730/2000 permutations (36.50%, 29.751453523766507 seconds remaining)
Job #1, processed 740/2000 permutations (37.00%, 29.49380746403256 seconds remaining)
Job #1, processed 750/2000 permutations (37.50%, 29.239944219589233 seconds remaining)
Job #1, processed 760/2000 permutations (38.00%, 28.975480594133074 seconds remaining)
Job #1, processed 770/2000 permutations (38.50%, 28.789680812265967 seconds remaining)
Job #1, processed 780/2000 permutations (39.00%, 28.601553537906746 seconds remaining)
Job #1, processed 790/2000 permutations (39.50%, 28.329947918276243 seconds remaining)
Job #1, processed 800/2000 permutations (40.00%, 28.087854981422424 seconds remaining)
Job #1, processed 810/2000 permutations (40.50%, 27.845355148668645 seconds remaining)
Job #1, processed 820/2000 permutations (41.00%, 27.595890836017887 seconds remaining)
Job #1, processed 830/2000 permutations (41.50%, 27.34862716801195 seconds remaining)
Job #1, processed 840/2000 permutations (42.00%, 27.11669131687709 seconds remaining)
Job #1, processed 850/2000 permutations (42.50%, 26.871561527252197 seconds remaining)
Job #1, processed 860/2000 permutations (43.00%, 26.646015178325563 seconds remaining)
Job #1, processed 870/2000 permutations (43.50%, 26.405459598563183 seconds remaining)
Job #1, processed 880/2000 permutations (44.00%, 26.200798121365633 seconds remaining)
Job #1, processed 890/2000 permutations (44.50%, 25.947382369737944 seconds remaining)
Job #1, processed 900/2000 permutations (45.00%, 25.725161817338734 seconds remaining)
Job #1, processed 910/2000 permutations (45.50%, 25.49724206295642 seconds remaining)
Job #1, processed 920/2000 permutations (46.00%, 25.260218195293263 seconds remaining)
Job #1, processed 930/2000 permutations (46.50%, 25.02660418069491 seconds remaining)
Job #1, processed 940/2000 permutations (47.00%, 24.782687922741502 seconds remaining)
Job #1, processed 950/2000 permutations (47.50%, 24.55623503735191 seconds remaining)
Job #1, processed 960/2000 permutations (48.00%, 24.309188524881996 seconds remaining)
Job #1, processed 970/2000 permutations (48.50%, 24.086994542289027 seconds remaining)
Job #1, processed 980/2000 permutations (49.00%, 23.841945414640467 seconds remaining)
Job #1, processed 990/2000 permutations (49.50%, 23.631085930448588 seconds remaining)
Job #1, processed 1000/2000 permutations (50.00%, 23.37639284133911 seconds remaining)
Job #1, processed 1010/2000 permutations (50.50%, 23.131427800301278 seconds remaining)
Job #1, processed 1020/2000 permutations (51.00%, 22.883953758314544 seconds remaining)
Job #1, processed 1030/2000 permutations (51.50%, 22.635330723327343 seconds remaining)
Job #1, processed 1040/2000 permutations (52.00%, 22.392945362971382 seconds remaining)
Job #1, processed 1050/2000 permutations (52.50%, 22.15560667855399 seconds remaining)
Job #1, processed 1060/2000 permutations (53.00%, 21.923991621665234 seconds remaining)
Job #1, processed 1070/2000 permutations (53.50%, 21.682650851312083 seconds remaining)
Job #1, processed 1080/2000 permutations (54.00%, 21.434762963542234 seconds remaining)
Job #1, processed 1090/2000 permutations (54.50%, 21.18981540749926 seconds remaining)
Job #1, processed 1100/2000 permutations (55.00%, 20.948660243641246 seconds remaining)
Job #1, processed 1110/2000 permutations (55.50%, 20.70929255786243 seconds remaining)
Job #1, processed 1120/2000 permutations (56.00%, 20.47000614234379 seconds remaining)
Job #1, processed 1130/2000 permutations (56.50%, 20.22918732398379 seconds remaining)
Job #1, processed 1140/2000 permutations (57.00%, 19.992007941530463 seconds remaining)
Job #1, processed 1150/2000 permutations (57.50%, 19.748085322587386 seconds remaining)
Job #1, processed 1160/2000 permutations (58.00%, 19.519276684728162 seconds remaining)
Job #1, processed 1170/2000 permutations (58.50%, 19.282667989404793 seconds remaining)
Job #1, processed 1180/2000 permutations (59.00%, 19.06325318853734 seconds remaining)
Job #1, processed 1190/2000 permutations (59.50%, 18.858939146795194 seconds remaining)
Job #1, processed 1200/2000 permutations (60.00%, 18.639429569244385 seconds remaining)
Job #1, processed 1210/2000 permutations (60.50%, 18.408319751093213 seconds remaining)
Job #1, processed 1220/2000 permutations (61.00%, 18.182857415715205 seconds remaining)
Job #1, processed 1230/2000 permutations (61.50%, 17.946419060714845 seconds remaining)
Job #1, processed 1240/2000 permutations (62.00%, 17.716460758639922 seconds remaining)
Job #1, processed 1250/2000 permutations (62.50%, 17.47511887550354 seconds remaining)
Job #1, processed 1260/2000 permutations (63.00%, 17.238388254528953 seconds remaining)
Job #1, processed 1270/2000 permutations (63.50%, 16.998182360581524 seconds remaining)
Job #1, processed 1280/2000 permutations (64.00%, 16.772903993725777 seconds remaining)
Job #1, processed 1290/2000 permutations (64.50%, 16.52914179757584 seconds remaining)
Job #1, processed 1300/2000 permutations (65.00%, 16.284806838402382 seconds remaining)
Job #1, processed 1310/2000 permutations (65.50%, 16.062797615546305 seconds remaining)
Job #1, processed 1320/2000 permutations (66.00%, 15.819139682885371 seconds remaining)
Job #1, processed 1330/2000 permutations (66.50%, 15.583037656052669 seconds remaining)
Job #1, processed 1340/2000 permutations (67.00%, 15.344255244553977 seconds remaining)
Job #1, processed 1350/2000 permutations (67.50%, 15.116956675494158 seconds remaining)
Job #1, processed 1360/2000 permutations (68.00%, 14.8789722218233 seconds remaining)
Job #1, processed 1370/2000 permutations (68.50%, 14.64620702458124 seconds remaining)
Job #1, processed 1380/2000 permutations (69.00%, 14.402063131332397 seconds remaining)
Job #1, processed 1390/2000 permutations (69.50%, 14.168373257136173 seconds remaining)
Job #1, processed 1400/2000 permutations (70.00%, 13.939272267477852 seconds remaining)
Job #1, processed 1410/2000 permutations (70.50%, 13.70778591074842 seconds remaining)
Job #1, processed 1420/2000 permutations (71.00%, 13.482662577024648 seconds remaining)
Job #1, processed 1430/2000 permutations (71.50%, 13.26562416970313 seconds remaining)
Job #1, processed 1440/2000 permutations (72.00%, 13.04395694202847 seconds remaining)
Job #1, processed 1450/2000 permutations (72.50%, 12.802775983152717 seconds remaining)
Job #1, processed 1460/2000 permutations (73.00%, 12.572234130885503 seconds remaining)
Job #1, processed 1470/2000 permutations (73.50%, 12.338668216653423 seconds remaining)
Job #1, processed 1480/2000 permutations (74.00%, 12.11029601097107 seconds remaining)
Job #1, processed 1490/2000 permutations (74.50%, 11.87578322583397 seconds remaining)
Job #1, processed 1500/2000 permutations (75.00%, 11.640702247619629 seconds remaining)
Job #1, processed 1510/2000 permutations (75.50%, 11.405179648999347 seconds remaining)
Job #1, processed 1520/2000 permutations (76.00%, 11.167212912910863 seconds remaining)
Job #1, processed 1530/2000 permutations (76.50%, 10.939802947387196 seconds remaining)
Job #1, processed 1540/2000 permutations (77.00%, 10.709682040400319 seconds remaining)
Job #1, processed 1550/2000 permutations (77.50%, 10.480985133878647 seconds remaining)
Job #1, processed 1560/2000 permutations (78.00%, 10.244616037760025 seconds remaining)
Job #1, processed 1570/2000 permutations (78.50%, 10.00742675848068 seconds remaining)
Job #1, processed 1580/2000 permutations (79.00%, 9.773532112942465 seconds remaining)
Job #1, processed 1590/2000 permutations (79.50%, 9.531504709015852 seconds remaining)
Job #1, processed 1600/2000 permutations (80.00%, 9.297566890716553 seconds remaining)
Job #1, processed 1610/2000 permutations (80.50%, 9.061887942485928 seconds remaining)
Job #1, processed 1620/2000 permutations (81.00%, 8.827872697217964 seconds remaining)
Job #1, processed 1630/2000 permutations (81.50%, 8.596997078211029 seconds remaining)
Job #1, processed 1640/2000 permutations (82.00%, 8.361844748985476 seconds remaining)
Job #1, processed 1650/2000 permutations (82.50%, 8.130254203622991 seconds remaining)
Job #1, processed 1660/2000 permutations (83.00%, 7.899152678179453 seconds remaining)
Job #1, processed 1670/2000 permutations (83.50%, 7.666537396208255 seconds remaining)
Job #1, processed 1680/2000 permutations (84.00%, 7.434536570594424 seconds remaining)
Job #1, processed 1690/2000 permutations (84.50%, 7.20293334249914 seconds remaining)
Job #1, processed 1700/2000 permutations (85.00%, 6.97075720394359 seconds remaining)
Job #1, processed 1710/2000 permutations (85.50%, 6.736010725735223 seconds remaining)
Job #1, processed 1720/2000 permutations (86.00%, 6.504483799601711 seconds remaining)
Job #1, processed 1730/2000 permutations (86.50%, 6.2703442642454466 seconds remaining)
Job #1, processed 1740/2000 permutations (87.00%, 6.03934129901316 seconds remaining)
Job #1, processed 1750/2000 permutations (87.50%, 5.805939878736223 seconds remaining)
Job #1, processed 1760/2000 permutations (88.00%, 5.573492418635975 seconds remaining)
Job #1, processed 1770/2000 permutations (88.50%, 5.340992472266073 seconds remaining)
Job #1, processed 1780/2000 permutations (89.00%, 5.110169574116053 seconds remaining)
Job #1, processed 1790/2000 permutations (89.50%, 4.878593117165166 seconds remaining)
Job #1, processed 1800/2000 permutations (90.00%, 4.648599094814724 seconds remaining)
Job #1, processed 1810/2000 permutations (90.50%, 4.4166660111253435 seconds remaining)
Job #1, processed 1820/2000 permutations (91.00%, 4.183536663160219 seconds remaining)
Job #1, processed 1830/2000 permutations (91.50%, 3.951979951128934 seconds remaining)
Job #1, processed 1840/2000 permutations (92.00%, 3.7201775675234585 seconds remaining)
Job #1, processed 1850/2000 permutations (92.50%, 3.4987791808875834 seconds remaining)
Job #1, processed 1860/2000 permutations (93.00%, 3.267092825264059 seconds remaining)
Job #1, processed 1870/2000 permutations (93.50%, 3.0343276485402315 seconds remaining)
Job #1, processed 1880/2000 permutations (94.00%, 2.801494542588579 seconds remaining)
Job #1, processed 1890/2000 permutations (94.50%, 2.5719030862132075 seconds remaining)
Job #1, processed 1900/2000 permutations (95.00%, 2.338553792551944 seconds remaining)
Job #1, processed 1910/2000 permutations (95.50%, 2.105655250749039 seconds remaining)
Job #1, processed 1920/2000 permutations (96.00%, 1.8713846802711487 seconds remaining)
Job #1, processed 1930/2000 permutations (96.50%, 1.6373079366634546 seconds remaining)
Job #1, processed 1940/2000 permutations (97.00%, 1.4035094718343204 seconds remaining)
Job #1, processed 1950/2000 permutations (97.50%, 1.1697760545290432 seconds remaining)
Job #1, processed 1960/2000 permutations (98.00%, 0.9355484368849774 seconds remaining)
Job #1, processed 1970/2000 permutations (98.50%, 0.7016087014057915 seconds remaining)
Job #1, processed 1980/2000 permutations (99.00%, 0.4678361488111092 seconds remaining)
Job #1, processed 1990/2000 permutations (99.50%, 0.23395763689549126 seconds remaining)
[Parallel(n_jobs=1)]: Done 1 out of 1 | elapsed: 46.8s finished
1970 detections
Total running time of the script: ( 1 minutes 30.773 seconds)
Estimated memory usage: 1984 MB